Problem:
Lines β1β and β2β both pass through the origin and make first-quadrant angles of 70Οβ and 54Οβ radians, respectively, with the positive x-axis. For any line β, the transformation R(β) produces another line as follows: β is reflected in β1β, and the resulting line is then reflected in β2β. Let R(1)(β)=R(β), and for integer nβ₯2 define R(n)(β)= R(R(nβ1)(β)). Given that β is the line y=9219βx, find the smallest positive integer m for which R(m)(β)=β.
Solution:
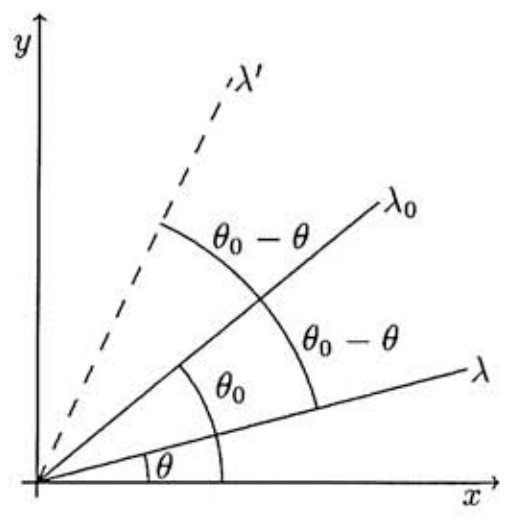
Let Ξ»0β and Ξ» be lines through the origin making angles of ΞΈ0β and ΞΈ, respectively, with the positive x-axis. When Ξ» is reflected in Ξ»0β, the resulting line Ξ»β² makes an angle of
ΞΈ0β+(ΞΈ0ββΞΈ)=2ΞΈ0ββΞΈ
with the positive x-axis. Thus, if Ξ» is reflected in β1β, then the result is a line Ξ»1β that passes through the origin and makes an angle of 270ΟββΞΈ with the positive x-axis. Reflecting Ξ»1β in the line β2β gives a line Ξ»2β through the origin that makes an angle of
254Οββ(270ΟββΞΈ)=β9458Οβ+ΞΈ
with the positive x-axis. Thus R(Ξ») is obtained by rotating Ξ» through β9458Οβ radians and R(m)(Ξ») is obtained by rotating Ξ» through β8mΟ/945 radians. For R(m)(Ξ»)=Ξ» to hold, 9458mβ must be an integer. The smallest positive integer value of m for which this is true is 945β.
The problems on this page are the property of the MAA's American Mathematics Competitions
