Problem:
Trapezoid ABCD has sides AB=92,BC=50,CD=19, and AD=70, with AB parallel to CD. A circle with center P on AB is drawn tangent to BC and AD. Given that AP=m/n, where m and n are relatively prime positive integers, find m+n.
Solution:
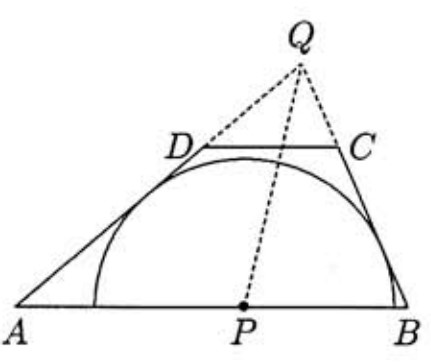
Extend AD and BC until the two segments meet at a point Q. Point P is equidistant from AQ and BQ, so P lies on the bisector of ∠AQB. Since the bisector of the angle of a triangle divides the side opposite the angle into segments whose lengths are proportional to the lengths of the adjoining sides, we have
BPAP=BQAQ=BCAD=57
Since AP+PB=92, it follows that AP=3161 and m+n=164.
OR
Label as E the point at which the circle is tangent to AD, and as F the point at which the circle is tangent to BC. Let G be the foot of the perpendicular from D to AB, and H the foot of the perpendicular from C to AB. Since PE=PF and DG=CH, it follows that
BPAP=21BP⋅CH21AP⋅DG=[PBC][APD]=21BC⋅FP21AD⋅EP=BCAD=57
Since AP+PB=92, it follows that AP=3161 and m+n=164.
The problems on this page are the property of the MAA's American Mathematics Competitions
.jpg)