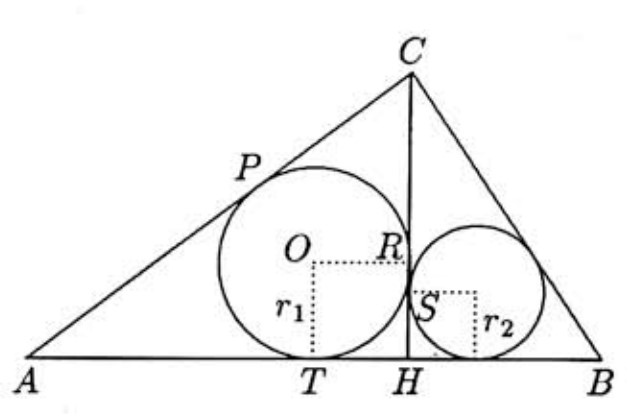
Problem:
Let CH be an altitude of △ABC. Let R and S be the points where the circles inscribed in triangles ACH and BCH are tangent to CH. If AB=1995,AC=1994, and BC=1993, then RS can be expressed as m/n, where m and n are relatively prime positive integers. Find m+n.
Solution:
Let a=BC,b=AC,c=AB,h=CH,p=AH, and q=BH. Let O be the center of the circle inscribed in △AHC, let r1 be the radius of this circle, and let T and P, respectively, be the points where this circle is tangent to AB and AC. Since ∠CHA is a right angle, we have OR⊥ OT, and hence RH=OT=r1. Similarly, SH=r2, where r2 is the radius of the circle inscribed in △CHB. Thus
RS=∣RH−SH∣=∣r1−r2∣
Next note that
b=AC=AP+CP=AT+CR=(p−r1)+(h−r1)
from which r1=(p+h−b)/2. Similarly, r2=(q+h−a)/2.
Thus
RS=∣r1−r2∣=∣∣∣∣∣2p+h−b−2q+h−a∣∣∣∣∣=21∣(p−q)+(a−b)∣(*)
By the Pythagorean Theorem, a2−q2=h2=b2−p2, so p2−q2=b2−a2. From this we have
p−q=p+q(b+a)(b−a)=c(b+a)(b−a)
Substituting this last expression into (∗) gives
RS=21∣∣∣∣∣c(b+a)(b−a)+(a−b)∣∣∣∣∣=2c∣b−a∣∣a+b−c∣
With a=1993,b=1994, and c=1995, we find
RS=2⋅199511992=665332
so m+n=332+665=997.
The problems on this page are the property of the MAA's American Mathematics Competitions