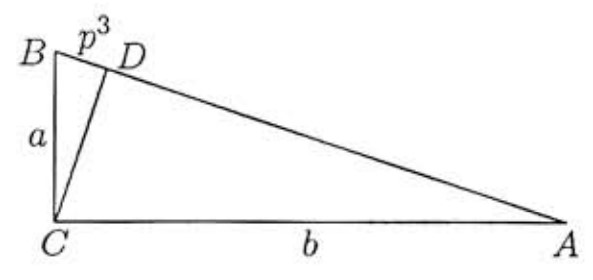
Problem:
In triangle ABC, angle C is a right angle and the altitude from C meets AB at D. The lengths of the sides of △ABC are integers, BD=293, and cosB=m/n, where m and n are relatively prime positive integers. Find m+n.
Solution:
Let a,b,c denote the lengths of BC,AC,AB, respectively. Let p=29, so BD=p3. Since △BCD∼△BAC we have
ap3=ca
from which a2=p3c. Since p is prime, there is an integer x such that c=px2. It follows that a=p2x. Substituting these expressions for a and c into b2=c2−a2 we find
b2=p2x4−p4x2=p2x2(x2−p2)
Thus, there is a positive integer y with x2−p2=y2, so p2=x2−y2=(x−y)(x+y). Since p is prime and x−y<x+y, we have x−y=1 and x+y=p2, which leads to
x=2p2+1 and y=2p2−1
Since p=29,
cosB=ca=px2p2x=(p2+1)/2p=(292+1)/229
in lowest terms. Hence m+n=(292+2⋅29+1)/2=(29+1)2/2=450.
The problems on this page are the property of the MAA's American Mathematics Competitions