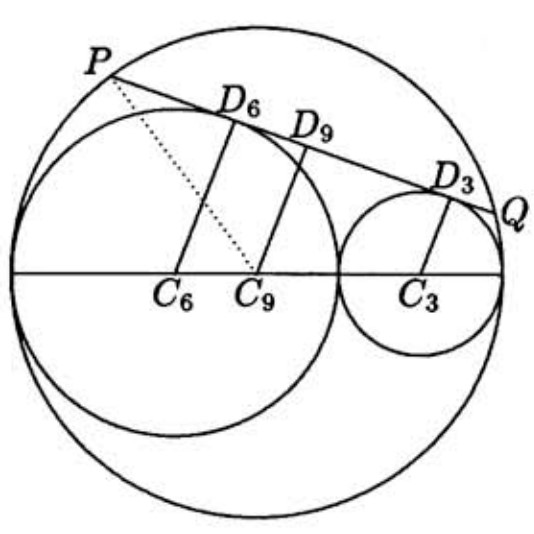
Problem:
Circles of radius 3 and 6 are externally tangent to each other and are internally tangent to a circle of radius 9. The circle of radius 9 has a chord that is a common external tangent of the other two circles. Find the square of the length of this chord.
Solution:
Let PQ be the tangent chord, and let C3,C6, and C9 be the centers of the circles of radii 3,6, and 9, respectively. We see that C6C9=3 and C9C3=6. Let D3,D6, and D9, respectively, be the feet of the perpendiculars from C3,C6, and C9 to PQ. Then D3 and D6 are points of tangency, and C3D3,C6D6, and C9D9 are parallel. It follows that
C9D9=31⋅C3D3+2⋅C6D6=5
Now apply the Pythagorean Theorem to right triangle C9PD9 to find that
(PQ)2=4(D9P)2=4[(C9P)2−(C9D9)2]=4(92−52)=224
The problems on this page are the property of the MAA's American Mathematics Competitions
.jpg)