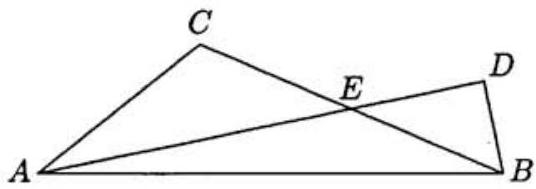
Problem: A B C , A B = 30 , A C = 6 A B C , A B = 3 0 , A C = 6 B C = 15 B C = 1 5 D D A D ‾ A D B C ‾ B C ∠ A D B ∠ A D B
Area ( △ A D B ) Area ( △ A B C ) A r e a ( △ A B C ) A r e a ( △ A D B )
can be written in the form m / n m / n m m n n m + n m + n
Solution:
Let A B = c , A C = b , B C = a A B = c , A C = b , B C = a a 2 + b 2 < c 2 a 2 + b 2 < c 2 ∠ C ∠ C D D △ A B C △ A B C A D A D B C ‾ B C E E B C ‾ B C B D ‾ B D B B △ A B E △ A B E
Area ( △ A D B ) Area ( △ A B C ) = Area ( △ A D B ) 2 Area ( △ A B E ) = 1 2 ( B D ) ( A D ) 2 ⋅ 1 2 ( B D ) ( A E ) = A D 2 A E (1) A r e a ( △ A B C ) A r e a ( △ A D B ) = 2 A r e a ( △ A B E ) A r e a ( △ A D B ) = 2 ⋅ 2 1 ( B D ) ( A E ) 2 1 ( B D ) ( A D ) = 2 A E A D ( 1 )
To find A E A E
b 2 = ( A E ) 2 + ( a 2 ) 2 − 2 ( A E ) ( a 2 ) cos ∠ C E A b 2 = ( A E ) 2 + ( 2 a ) 2 − 2 ( A E ) ( 2 a ) cos ∠ C E A
and
c 2 = ( A E ) 2 + ( a 2 ) 2 − 2 ( A E ) ( a 2 ) cos ∠ A E B c 2 = ( A E ) 2 + ( 2 a ) 2 − 2 ( A E ) ( 2 a ) cos ∠ A E B
Now add these two equations, using the fact that cos ∠ C E A + cos ∠ A E B = 0 cos ∠ C E A + cos ∠ A E B = 0 A E A E
A E = 1 2 2 b 2 + 2 c 2 − a 2 A E = 2 1 2 b 2 + 2 c 2 − a 2
Apply the Pythagorean Theorem to find that
( A D ) 2 + ( B D ) 2 = c 2 ( A D ) 2 + ( B D ) 2 = c 2
and
( D E ) 2 + ( B D ) 2 = 1 4 a 2 ( D E ) 2 + ( B D ) 2 = 4 1 a 2
Substitute A D = A E + E D A D = A E + E D
to find ( A E ) 2 + 2 ( A E ) ( E D ) = c 2 − 1 4 a 2 ( A E ) 2 + 2 ( A E ) ( E D ) = c 2 − 4 1 a 2
Thus
E D 2 A E = c 2 − 1 4 a 2 − ( A E ) 2 4 ( A E ) 2 = c 2 − b 2 2 ( 2 b 2 + 2 c 2 − a 2 ) 2 A E E D = 4 ( A E ) 2 c 2 − 4 1 a 2 − ( A E ) 2 = 2 ( 2 b 2 + 2 c 2 − a 2 ) c 2 − b 2
Return to ( 1 ) ( 1 )
Area ( △ A D B ) Area ( △ A B C ) = A E + E D 2 A E = 1 2 + E D 2 A E A r e a ( △ A B C ) A r e a ( △ A D B ) = 2 A E A E + E D = 2 1 + 2 A E E D
When a = 15 , b = 6 a = 1 5 , b = 6 c = 30 c = 3 0 1 2 + 4 19 = 27 38 2 1 + 1 9 4 = 3 8 2 7 m + n = 65 m + n = 6 5
The problems on this page are the property of the MAA's American Mathematics Competitions