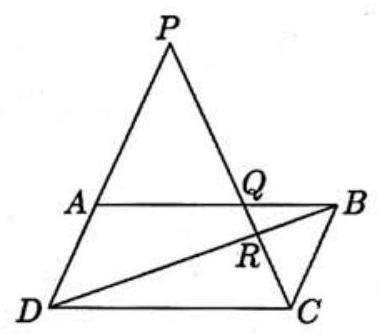
Problem:
Let ABCD be a parallelogram. Extend DA though A to a point P, and let PC meet AB at Q and DB at R. Given that PQ=735 and QR=112, find RC.
Solution:
The similarity of triangles RBC and RDP implies that RPRC=RDRB, and the similarity of triangles RBQ and RDC implies that RDRB=RCRQ. Thus RPRC=RCRQ, or RC2=RQ⋅RP=112⋅847=16⋅7⋅7⋅121. Hence RC=4⋅7⋅11=308.
The problems on this page are the property of the MAA's American Mathematics Competitions