Problem:
A function f is defined on the complex numbers by f(z)=(a+bi)z, where a and b are positive numbers. This function has the property that the image of each point in the complex plane is equidistant from that point and the origin. Given that β£a+biβ£=8 and that b2=m/n, where m and n are relatively prime positive integers, find m+n.
Solution:
Because (a+bi)z is equidistant from z and 0,β£(a+bi)zβzβ£=β£(a+bi)zβ£. Thus β£aβ1+biβ£=β£a+biβ£, or (aβ1)2+b2=a2+b2, so a=21β. Now use the information β£a+biβ£=8 to deduce that b2=64β41β=4255β, so that m+n=259β.
OR
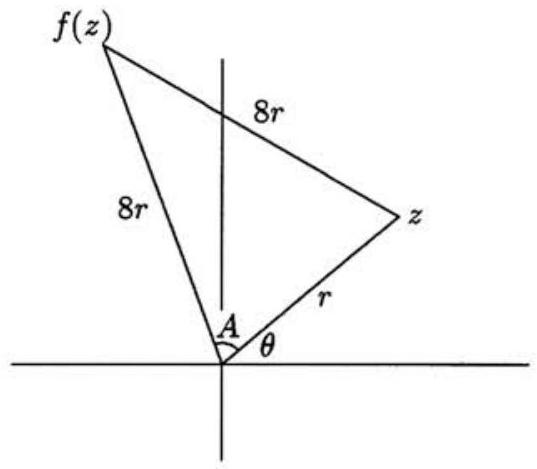
Let z=rcisΞΈ=r(cosΞΈ+isinΞΈ), where r is positive and 0β€ΞΈ<2Ο, and let a+bi=8cisA, where 0<A<Ο/2. Thus f(z)=8rcis(ΞΈ+A). Notice that cosA=8rr/2β=161β, because the triangle in the figure is isosceles. It follows that
b2=82sin2A=64(1βcos2A)=4255β.
Thus m+n=259β.
The problems and solutions on this page are the property of the MAA's American Mathematics Competitions
