Problem:
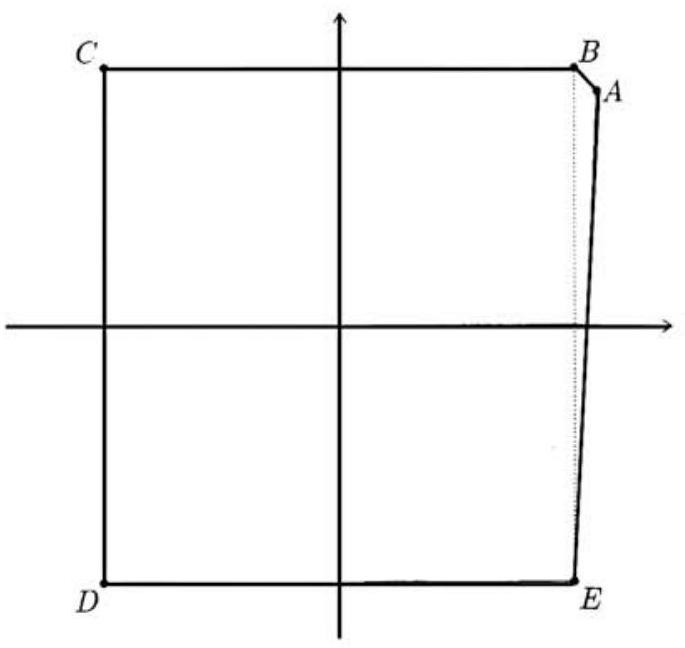
Let u and v be integers satisfying 0<v<u. Let A=(u,v), let B be the reflection of A across the line y=x, let C be the reflection of B across the y-axis, let D be the reflection of C across the x-axis, and let E be the reflection of D across the y-axis. The area of the pentagon ABCDE is 451. Find u+v.
Solution:
It follows from the problem statement that the coordinates of A,B,C,D, and E are A=(u,v),B=(v,u),C=(−v,u),D=(−v,−u), and E=(v,−u). The pentagon can be partitioned into rectangle BCDE and triangle ABE, whose areas are 2u⋅2v=4uv and 212u(u−v)=u2−uv, so
Area(ABCDE)=4uv+u2−uv=u(3v+u)
Thus u(3v+u)=451=11⋅41. Because 0<v<u, it follows that u=11,3v+11=41, v=10, and u+v=21.
The problems on this page are the property of the MAA's American Mathematics Competitions
