¶ 2001 AIME I Problem 13
Problem:
In a certain circle, the chord of a -degree arc is centimeters long, and the chord of a -degree arc is centimeters longer than the chord of a -degree arc, where . The length of the chord of a -degree arc is centimeters, where and are positive integers. Find .
Solution:
In the figure, points , and are concyclic, the degree sizes of arcs , and are all , and . Note that is the chord of a -degree arc. Let . Then , because is the chord of a -degree arc. In isosceles trapezoid , draw the altitude from to , and notice that divides into and . Because the right triangles and share the leg , it follows that
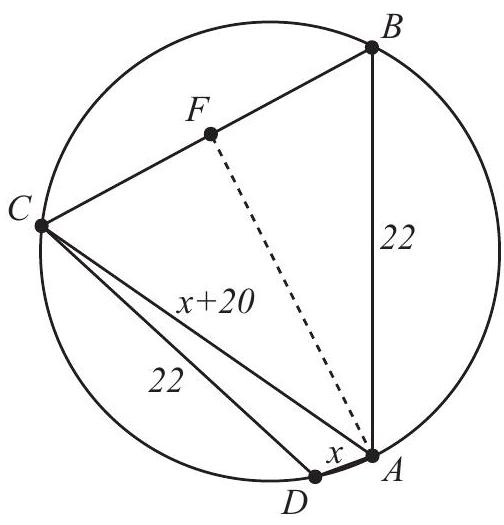
which simplifies to . Thus and .
Noting that is a cyclic isosceles trapezoid, apply Ptolemy's Theorem to obtain , or . Solve the equation to find that .
Query: If the restriction were removed, then the problem would have an additional solution. Can you find it?
The problems and solutions on this page are the property of the MAA's American Mathematics Competitions