¶ 2001 AIME I Problem 4
Problem:
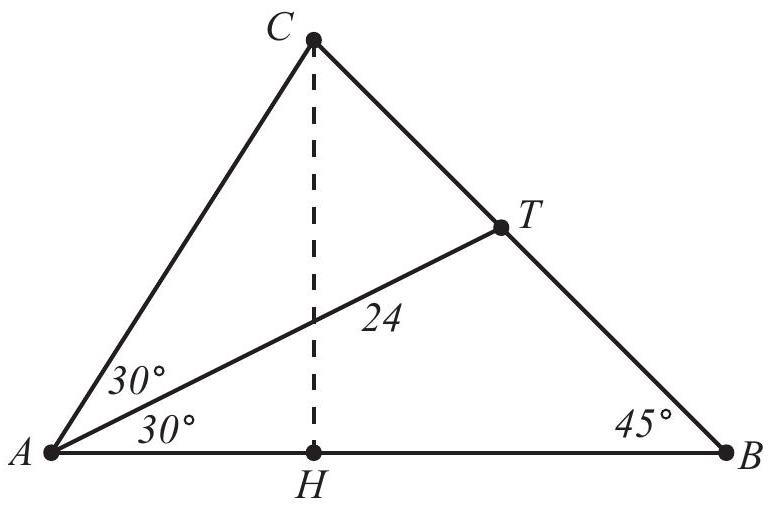
In triangle , angles and measure degrees and degrees, respectively. The bisector of angle intersects at , and . The area of the triangle can be written in the form , where , and are positive integers, and is not divisible by the square of any prime. Find .
Solution:
Note that angles and each measure , so . Draw altitude of triangle . Then triangle is and triangle is . Now and . The area of triangle is thus .
Answer:
The problems on this page are the property of the MAA's American Mathematics Competitions