Problem:
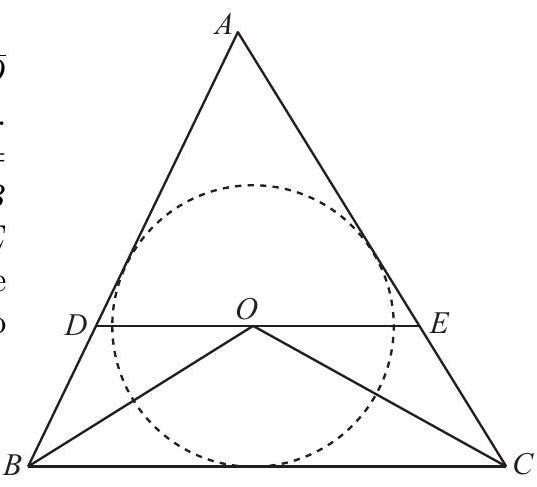
Triange ABC has AB=21,AC=22, and BC=20. Points D and E are located on AB and AC, respectively, such that DE is parallel to BC and contains the center of the inscribed circle of triangle ABC. Then DE=m/n, where m and n are relatively prime positive integers. Find m+n.
Solution:
Let O be the incenter of triangle ABC, so that BO and CO bisect angles ABC and ACB, respectively. Because DE is parallel to BC, it follows that ∠DOB= ∠DBO and ∠EOC=∠ECO, hence that DO=DB and EO=EC. Thus the perimeter if triangle ADE is AB+AC. Triangle ADE is similar to triangle ABC, with the ratio of similarity equal to the ratio of perimeters. Therefore
BCDE=AB+AC+BCAB+AC
Substituting the given values yields DE=860/63, and m+n=923.
OR
Let r be the radius of the inscribed circle, and h be the length of the altitude from A to BC. Then the area of triangle ABC may be computed in two ways as
21BC⋅h=21(AB+AC+BC)r, so that hr=AB+AC+BCBC
Triangles ADE and ABC are similar, their ratio of similarity equal to the ratio of any pair of corresponding altitudes. Therefore
DE=hh−rBC=AB+AC+BC(AB+AC)BC
As above, m+n=923.
The problems on this page are the property of the MAA's American Mathematics Competitions