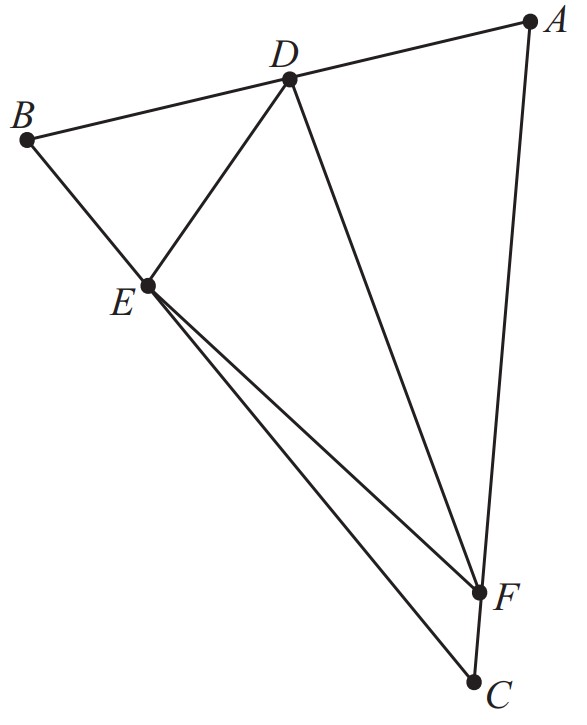
Problem:
In triangle ABC,AB=13,BC=15 and CA=17. Point D is on AB,E is on BC, and F is on CA. Let AD=p⋅AB,BE=q⋅BC, and CF=r⋅CA, where p,q, and r are positive and satisfy p+q+r=2/3 and p2+q2+r2=2/5. The ratio of the area of triangle DEF to the area of triangle ABC can be written in the form m/n, where m and n are relatively prime positive integers. Find m+n.
Solution:
Let [XYZ] denote the area of triangle XYZ. Because p,q, and r are all smaller than 1 , it follows that
[BDE][EFC][ADF][ABC][ABC][DEF]=q(1−p)[ABC]=r(1−q)[ABC]=p(1−r)[ABC]=[DEF]+[BDE]+[EFC]+[ADF]=[DEF]+((p+q+r)−(pq+qr+rp))[ABC], and =1+pq+qr+rp−(p+q+r)
Note that
pq+qr+rp=21[(p+q+r)2−(p2+q2+r2)]=21(94−52)=451
Thus the desired ratio is 1+451−32=4516 and m+n=61
The problems on this page are the property of the MAA's American Mathematics Competitions