¶ 2001 AIME II Problem 6
Problem:
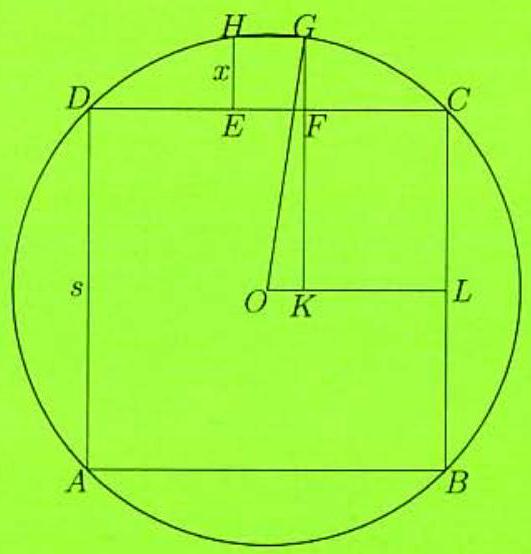
Square is inscribed in a circle. Square has vertices and on and vertices and on the circle. The ratio of the area of square to the area of square can be expressed as where and are relatively prime positive integers and . Find .
Solution:
Let be the center of the circle, and represent the lengths of each side of the small square and the large square by and , respectively. Draw perpendicular to at and perpendicular to at . Then , and the circle's radius is . Applying the Pythagorean Theorem to triangle , we obtain . Expanding yields which leads to , or , so . The ratio of the squares' areas is thus , and .
The problems on this page are the property of the MAA's American Mathematics Competitions