Problem:
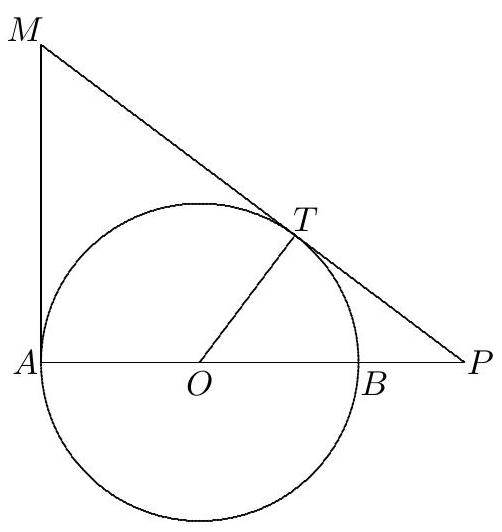
The perimeter of triangle APM is 152 , and angle PAM is a right angle. A circle of radius 19 with center O on AP is drawn so that it is tangent to AM and PM. Given that OP=m/n, where m and n are relatively prime positive integers, find m+n.
Solution:
Let T and B be the points where the circle meets PM and AP, respectively, with ABP. Triangles POT and PAM are right triangles that share angle MPA, so they are similar. Let p1 and p2 be their respective perimeters. Then OT/AM=p1/p2. Because AM=TM, it follows that p1=p2−(AM+TM)=152−2AM. Thus 19/AM=(152−2AM)/152, so that AM=38 and p1=76. It is also true that OP/PM=p1/p2, so
21=PMOP=152−(38+19+OP)OP
It follows that OP=95/3, and m+n=98.
The problems on this page are the property of the MAA's American Mathematics Competitions