¶ 2004 AIME I Problem 10
Problem:
A circle of radius is randomly placed in a -by- rectangle so that the circle lies completely within the rectangle. Given that the probability that the circle will not touch diagonal is , where and are relatively prime positive integers, find .
Solution:
In order for the circle to lie completely within the rectangle, the center of the circle must lie in a rectangle that is by or by . The requested probability is equal to the probability that the distance from the circle's center to the diagonal is greater than , which equals the probability that the distance from a randomly selected point in the -by- rectangle to each of the sides of and is greater than . Let and . Draw the three line segments that are one unit respectively from each of the sides of and whose endpoints are on the sides. Let , and be the three points of intersection nearest to , and , respectively, of the three line segments. Let be the intersection of and , and let and be the projections of and on and , respectively. Then . Notice that and , so . Similarly, and , so .
Thus
Apply the Pythagorean Theorem to to obtain . Substitute these lengths to find that . Notice that , and their similarity ratio is , so . The requested probability is therefore
so .
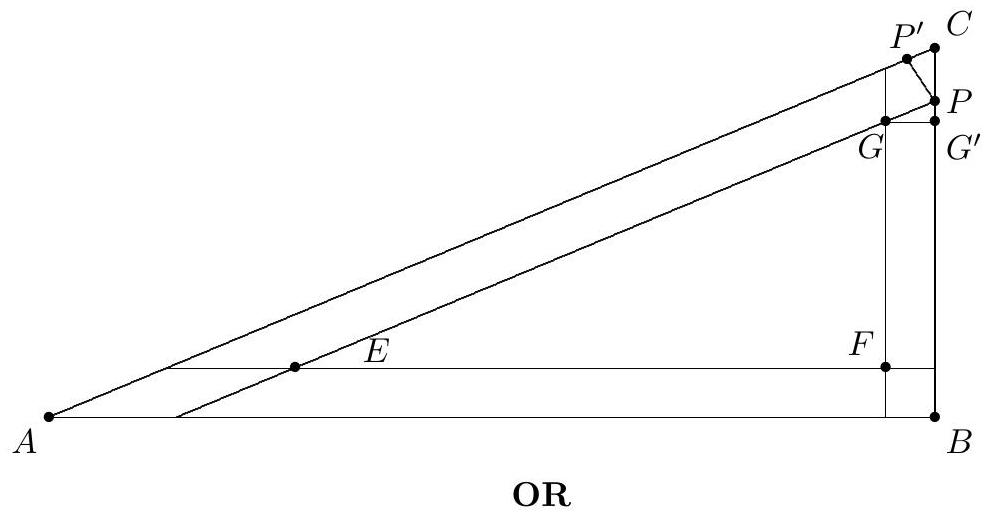
Define , and as in the previous solution. Each of these three points is equidistant from two sides of , and they are therefore on the anglebisectors of angles , and , respectively. These angle-bisectors are also angle-bisectors of because its sides are parallel to those of . Thus and have the same incenter, and the inradius of is one less than that of . In general, the inradius of a triangle is the area divided by one-half the perimeter, so the inradius of is . The similarity ratio of to is the same as the ratio of their inradii, namely . Continue as in the previous solution.
Define , and as in the previous solutions. Notice that bisects and that , and so, by the Half-Angle Formula, . Thus, for some and . Apply the Pythagorean Theorem in to conclude that , so . Then , and . Continue as in the first solution.
The problems on this page are the property of the MAA's American Mathematics Competitions