Problem:
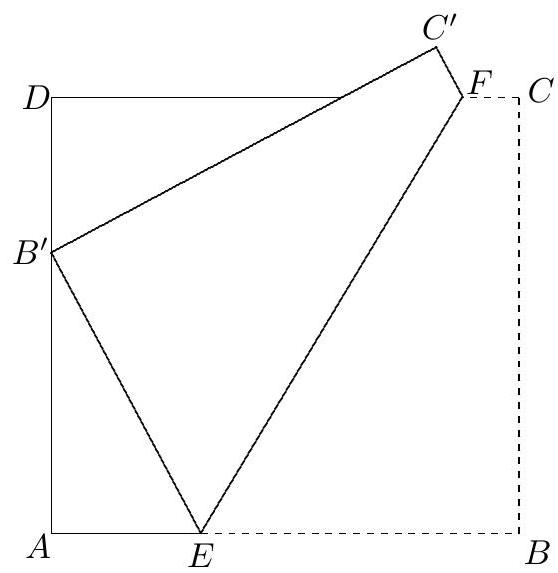
ABCD is a rectangular sheet of paper that has been folded so that corner B is matched with point B′ on edge AD. The crease is EF, where E is on AB and F is on CD. The dimensions AE=8,BE=17, and CF=3 are given. The perimeter of rectangle ABCD is m/n, where m and n are relatively prime positive integers. Find m+n.
Solution:
Let B′C′ and CD intersect at H. Note that B′E=BE=17. Apply the Pythagorean Theorem to △EAB′ to obtain AB′=15. Because ∠C′ and ∠C′B′E are right angles, △B′AE∼△HDB′∼△HC′F, so the lengths of the sides of each triangle are in the ratio 8:15:17. Now C′F=CF=3 implies that FH=(17/8)3=51/8 and DH=25−(3+51/8)=125/8. Then B′D=(8/15)(125/8)=25/3. Thus AD=70/3, and the perimeter of ABCD is
2⋅25+2⋅370=3290
so m+n=290+3=293.
OR
Notice first that B′E=BE=17. Apply the Pythagorean Theorem to △EAB′ to obtain AB′=15. Draw FG parallel to CB, with G on AB. Notice that GE=17−3=14. Because points on the crease EF are equidistant from B and B′, it follows that EF is perpendicular to BB′, and hence that triangles EGF and B′AB are similar. In particular, BAFG=AB′GE. This yields FG=70/3, and the perimeter of ABCD is therefore 290/3.
The problems and solutions on this page are the property of the MAA's American Mathematics Competitions