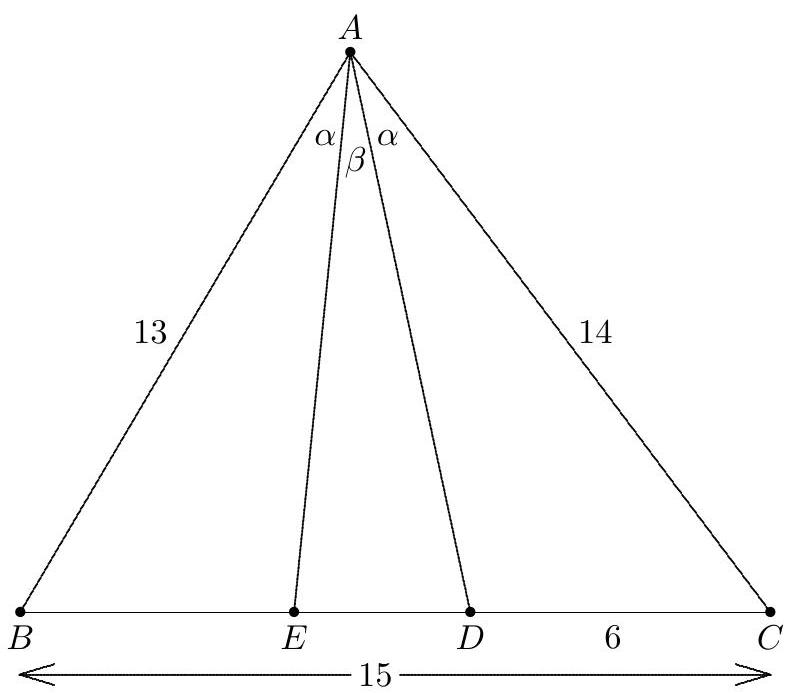
Problem:
In β³ABC,AB=13,BC=15, and CA=14. Point D is on BC with CD=6. Point E is on BC such that β BAEβ
β CAD. Given that BE=p/q, where p and q are relatively prime positive integers, find q.
Solution:
Let mβ BAE=Ξ±=mβ CAD, and let Ξ²=mβ EAD. Then
DCBDβ=[ADC][ABD]β=(1/2)ADβ
ACsinCAD(1/2)ABβ
ADsinBADβ=ACABββ
sinΞ±sin(Ξ±+Ξ²)β
Similarly,
ECBEβ=ACABββ
sinCAEsinBAEβ=ACABββ
sin(Ξ±+Ξ²)sinΞ±β
and so
ECBEβ=AC2β
BDAB2β
DCβ
Substituting the given values yields BE/EC=(132β
6)/(142β
9)=169/294. Therefore BE=(15β
169)/(169+294)=(3β
5β
132)/463. Because none of 3,5, and 13 divides 463,q=463β.
The problems on this page are the property of the MAA's American Mathematics Competitions
