Problem:
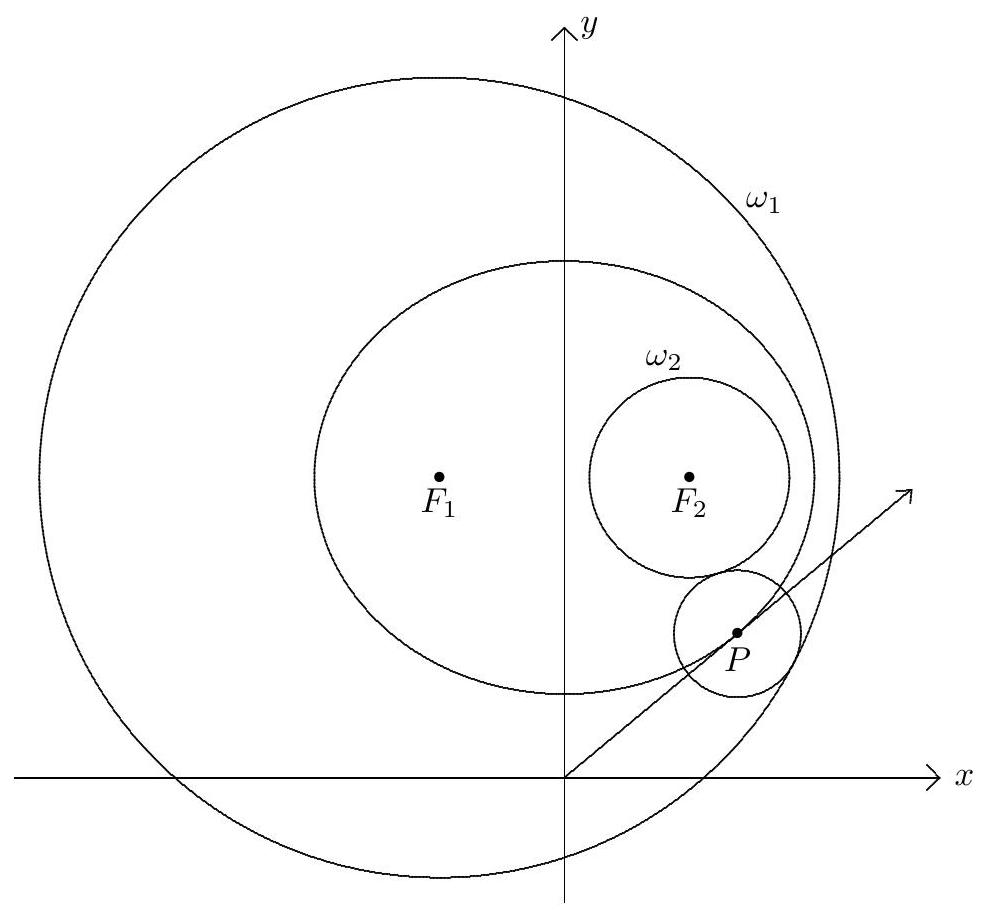
Let Ο1β and Ο2β denote the circles x2+y2+10xβ24yβ87=0 and x2+y2β 10xβ24y+153=0, respectively. Let m be the smallest positive value of a for which the line y=ax contains the center of a circle that is internally tangent to Ο1β and externally tangent to Ο2β. Given that m2=p/q, where p and q are relatively prime positive integers, find p+q.
Solution:
Complete the square to obtain (x+5)2+(yβ12)2=256 and (xβ5)2+(yβ12)2=16 for Ο1β and Ο2β, respectively. Hence Ο1β is centered at F1β(β5,12) with radius 16 , and Ο2β is centered at F2β(5,12) with radius 4. Let P be the center of the third circle, and let r be its radius. Then PF1β=16βr and PF2β=4+r. Thus P is on the ellipse with foci F1β,F2β and PF1β+PF2β=20. Therefore the coordinates of P satisfy
100x2β+75(yβ12)2β=1
which is equivalent to 3x2+4y2β96y+576=300. Because P is on the line with equation y=ax, conclude that the x-coordinate of P satisifies
(3+4a2)x2β96ax+276=0
In order for P to exist, the discriminant of the above quadratic equation must be nonnegative, that is, (β96a)2β4β
276β
(4a2+3)β₯0. Thus a2β₯69/100, so m2=69/100, and p+q=169β.
Note that a attains its minimum when the line with equation y=ax is tangent to the ellipse.
The problems on this page are the property of the MAA's American Mathematics Competitions
