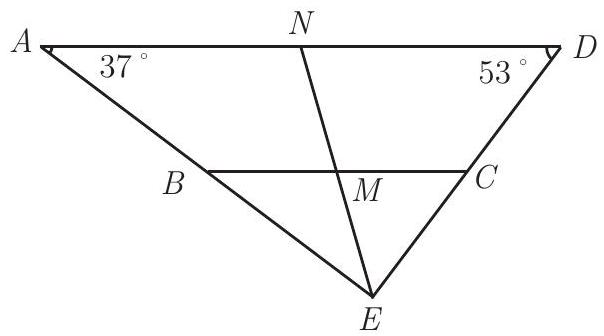
Problem:
In trapezoid ABCD with BC∥AD, let BC=1000 and AD=2008. Let ∠A=37∘,∠D=53∘, and M and N be the midpoints of BC and AD, respectively. Find the length MN.
Solution:
Extend leg AB past B and leg CD past C, and let E be the point of intersection of these extensions. Then because ANBM=DNCM, line MN must pass through point E. But ∠A=37∘ and ∠D=53∘ implies that ∠AED=90∘. Thus △EDA is a right triangle with median EN, and △EBC is a right triangle with median EM. The median to the hypotenuse in any right triangle is half the hypotenuse, so EN=22008=1004,EM=21000=500, and MN=EN−EM=504.
The problems on this page are the property of the MAA's American Mathematics Competitions