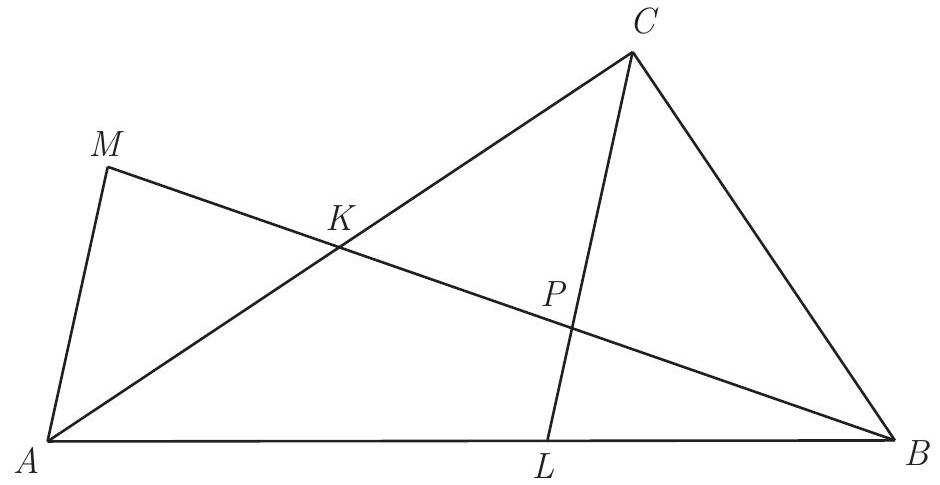
Problem:
Triangle ABC has AC=450 and BC=300. Points K and L are located on AC and AB respectively so that AK=CK, and CL is the angle bisector of angle C. Let P be the point of intersection of BK and CL, and let M be the point on line BK for which K is the midpoint of PM. If AM=180, find LP.
Solution:
Because the diagonals of APCM bisect each other, APCM is a parallelogram. Thus AM is parallel to CP. Because △ABM is similar to △LBP, LPAM=BLAB=1+BLAL. Apply the Angle Bisector Theorem in triangle ABC to obtain BLAL=BCAC. Therefore LPAM=1+BCAC, and LP=AC+BCAM⋅BC. Thus LP=450+300180⋅300=72.
The problems on this page are the property of the MAA's American Mathematics Competitions