¶ 2011 AIME I Problem 4
Problem:
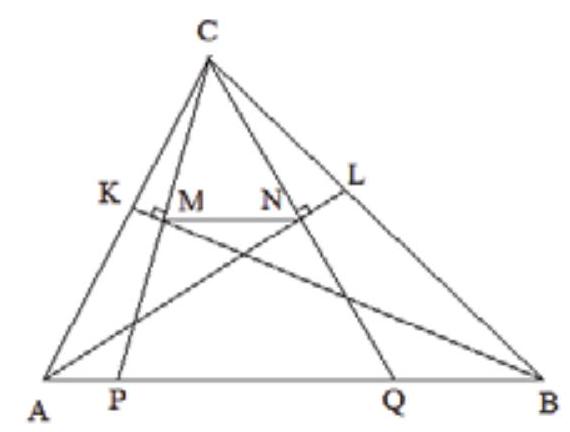
In triangle , and . The angle bisector of angle intersects at point , and the angle bisector of angle intersects at point . Let and be the feet of the perpendiculars from to and , respectively. Find .
Solution:
Extend and to meet at points and , respectively. Triangles and are congruent. Thus is the midpoint of . Analogously, is the midpoint of . Hence is a midline of triangle , and . Furthermore,
Thus .
The problems on this page are the property of the MAA's American Mathematics Competitions