¶ 2011 AIME I Problem 8
Problem:
In , and . Points and are on with on , points and are on with on , and points and are on with on . In addition, the points are positioned so that , and . Right angle folds are then made along , and . The resulting figure is placed on a level floor to make a table with triangular legs. Let be the maximum possible height of a table constructed from whose top is parallel to the floor. Then can be written in the form , where and are relatively prime positive integers and is a positive integer that is not divisible by the square of any prime. Find .
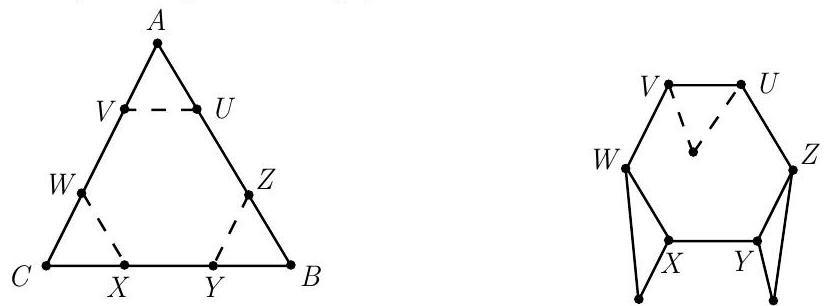
Solution:
Call a table functional if its top is parallel to the floor. Let , , and , with . The height of a functional table is the common height of triangles , and , where each height is measured to the fold. For a functional table to be of maximum height, two of the folds must intersect on a side of the triangle. If this were not the case, then each fold could be shifted by the same small amount to obtain a functional table with greater height. Thus , or . Assume that . Let the common height of and be , and let , so that . Because is similar to , it follows that and .
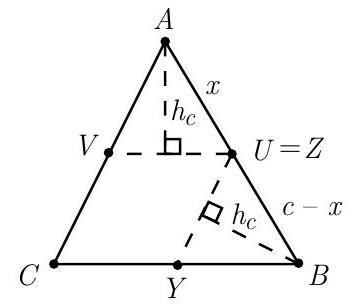
Thus
Similarly, by using , it follows that . Equating these two expressions and solving for yields , and hence . By similar arguments, the heights and that result from and , respectively, are
Thus the maximum height of a functional table is the minimum of , and , which is , because if the height were larger than this, some of the folds would intersect.
For the given triangle, , and , and by Heron's Formula, . Because the two longer sides have lengths 27 and 30 , the formula yields
and the required sum is .
The problems on this page are the property of the MAA's American Mathematics Competitions