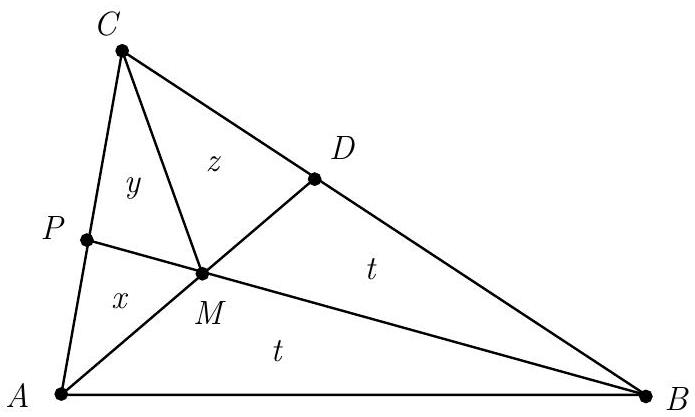
Problem:
In triangle ABC,AB=1120AC. The angle bisector of ∠A intersects BC at point D, and point M is the midpoint of AD. Let P be the point of intersection of AC and line BM. The ratio of CP to PA can be expressed in the form nm, where m and n are relatively prime positive integers. Find m+n.
Solution:
Let [AMP]=x,[CMP]=y,[CMD]=z, and [BMD]=t.
Because M is the midpoint of AD, it follows that [AMB]=[BMD]=t.
The Angle Bisector Theorem yields
tz=BDCD=ABAC=2011
Also,
[CBM][CPM]=MBPM=[ABM][APM], or z+ty=tx.
Thus
PACP=xy=tz+t=tz+1=2011+1=2031
Hence m+n=51.
OR
Through D draw a parallel to line BP intersecting line AC at Q. Then PQ=20k,QC=11k, and PA=20k, using the Angle Bisector Theorem and the fact that 3 or more parallel lines divide all transversals in the same proportions. Thus PACP=20k20k+11k=2031 as in the previous solution.