¶ 2012 AIME I Problem 8
Problem:
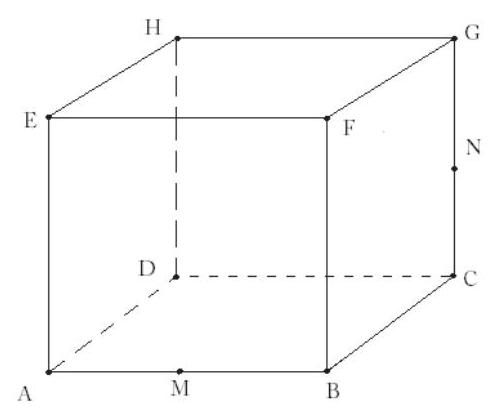
Cube , labeled as shown below, has edge length and is cut by a plane passing through vertex and the midpoints and of and , respectively. The plane divides the cube into two solids. The volume of the larger of the two solids can be written in the form , where and are relatively prime positive integers. Find .
Solution:
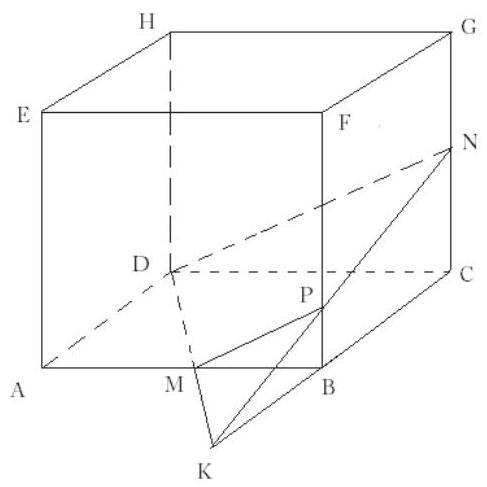
Let the plane intersect at point and the extension of at point . Because is the midpoint of and is parallel to , it follows that is the midpoint of and therefore . Hence the volume of the pyramid is equal to . Because is similar to with a constant of proportionality of , the volume of is , and the volume of is . Thus the volume of the larger solid is , and .
The problems on this page are the property of the MAA's American Mathematics Competitions