¶ 2012 AIME II Problem 5
Problem:
In the accompanying figure, the outer square has side length . A second square of side length is constructed inside with the same center as and with sides parallel to those of . From each midpoint of a side of , segments are drawn to the two closest vertices of . The result is a four-pointed starlike figure inscribed in . The star figure is cut out and then folded to form a pyramid with base . Find the volume of this pyramid.
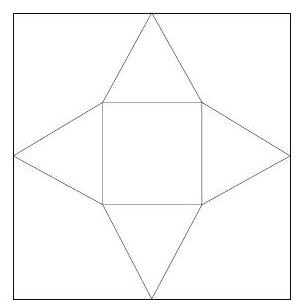
Solution:
Let be the vertex of the pyramid, let be the center of , and let be the midpoint of one of the sides of . Then the height of the pyramid is , and the volume of the pyramid is . Note that is a right triangle with hypotenuse and . Therefore
Hence the volume of the pyramid is .
The problems on this page are the property of the MAA's American Mathematics Competitions