¶ 2013 AIME I Problem 3
Problem:
Let be a square, and let and be points on and , respectively. The line through parallel to and the line through parallel to divide into two squares and two nonsquare rectangles. The sum of the areas of the two squares is of the area of square . Find .
Solution:
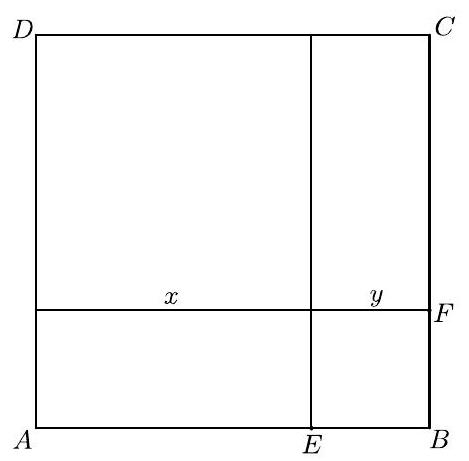
Let the sides of the two smaller squares have lengths and so that the square has side length . It is given that . Then , and . The requested sum is .
The problems on this page are the property of the MAA's American Mathematics Competitions