¶ 2013 AIME I Problem 9
Problem:
A paper equilateral triangle has side length . The paper triangle is folded so that vertex touches a point on side a distance from point . The length of the line segment along which the triangle is folded can be written as , where , and are positive integers, and are relatively prime, and is not divisible by the square of any prime. Find .
Solution:
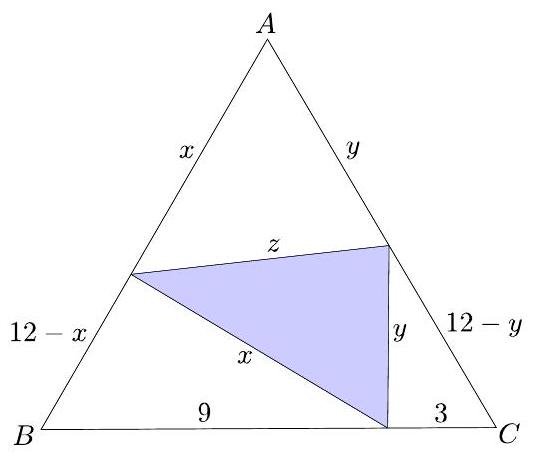
Let the fold line intersect sides and at distances and from point , respectively, as shown. Let the fold line have length . Then the Law of Cosines gives , which simplifies to . Similarly, , which simplifies to .
Finally, , which simplifies to . The requested sum is .
The problems on this page are the property of the MAA's American Mathematics Competitions