¶ 2013 AIME II Problem 8
Problem:
A hexagon that is inscribed in a circle has side lengths , and in that order. The radius of the circle can be written as , where and are positive integers. Find .
Solution:
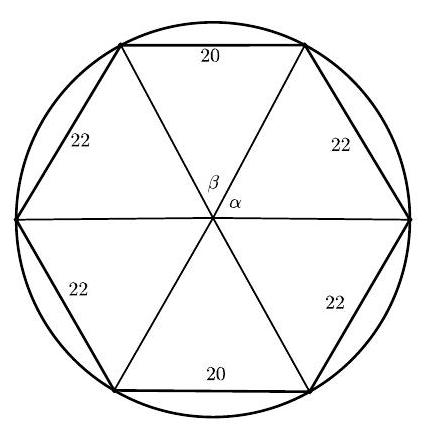
Let be the radius of the circle, let be the central angle of each arc cut off by chords of length , and let be the central angle of each arc cut off by chords of length . Then . Thus and are complementary angles, so that .
By the Law of Cosines, , so . Note that .
Together these observations give the equation
which implies
The solutions are . Only the positive sign gives a positive value of . The requested sum is .
Note that any diagonal of the hexagon that connects opposite vertices is a diameter of the circle. Let be the isosceles trapezoid where , and is a diameter of the circle. Let the center of the circle be , and let be a point on such that . Apply the Pythagorean Theorem to to get , and to to get . Given that and , conclude that and , which is the same equation as in the previous solution.
The problems and solutions on this page are the property of the MAA's American Mathematics Competitions