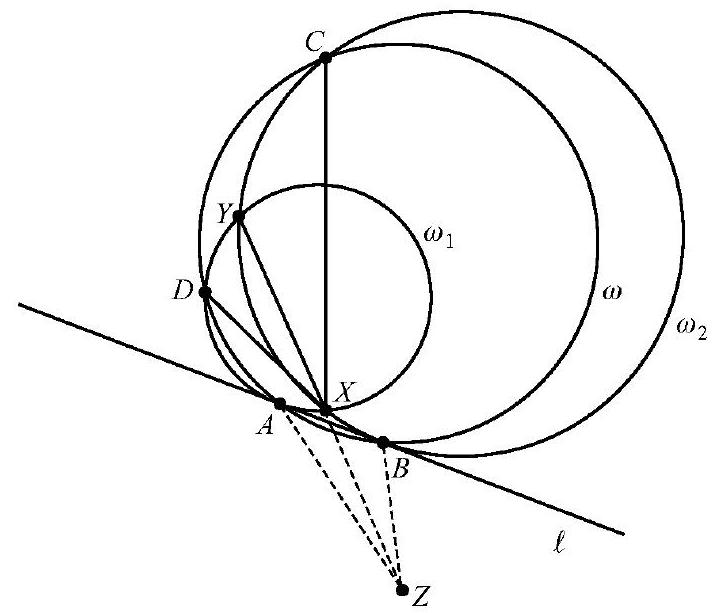
Problem:
Circles Ο1β and Ο2β intersect at points X and Y. Line β is tangent to Ο1β and Ο2β at A and B, respectively, with line AB closer to point X than to Y. Circle Ο passes through A and B intersecting Ο1β again at Dξ =A and intersecting Ο2β again at Cξ =B. The three points C,Y, and D are collinear, XC=67,XY=47, and XD=37. Find AB2.
Solution:
Note that lines AD,XY,BC are the radical axes of pairs of circles Ο and Ο1β, Ο1β and Ο2β,Ο2β and Ο, respectively. Therefore lines AD,XY, and BC are either parallel to each other or concurrent. In the former case, Ο1β and Ο2β would be the same size, and by symmetry, CX=DX, contradicting the given condition. Hence it must be that lines AD,XY, and BC are concurrent at a point Z. Denote by M the intersection of segments ZY and AB. By the Power of a Point Theorem it follows that MA2=MXβ
MY=MB2. In particular,
AB2β=4MA2=4MXβ
MY=4MX(MX+XY)=(2MX+XY)2βXY2=(MY+MX)2βXY2β
Claim: (MX+MY)2=CXβ
DX. The claim implies that AB2=CXβ
DXβ XY2=37β
67β472=270β.
The proof of the claim is based on the following three observations: ZAXB is cyclic; β³XZC is similar to β³XDZ; and ZAYB is a parallelogram.
Because BCYX is cyclic, β XBZ=β XYC. Because ADYX is cyclic, β XAZ= β XYD. Because C,Y, and D are collinear, β XAZ+β XBZ=β XYD+ β XYC=180β, from which it follows that ZAXB is cyclic, establishing the first observation. This is also a direct consequence of Miquel's Theorem.
Because BCYX and ZAXB are cyclic, β XCB=β XYB and β ABX= β AZX. Because AB is tangent to Ο2β at B,β ABX=β XYB. Combining the three equations yields β XCZ=β XCB=β XYB=β ABX=β AZX= β DZX. Likewise, β XZC=β XDZ. Hence β³XZC is similar to β³XDZ, establishing the second observation.
As in the previous paragraph, β XYB=β AZX or BYβ₯AZ. Similarly, AYβ₯ BZ. Thus ZAYB is a parallelogram, establishing the third observation.
Because ZAYB is a parallelogram, MY=MZ and MX+MY=XM+MZ= XZ. Because β³XZC and β³XDZ are similar, XCXZβ=XZXDβ or XZ2=XCβ
XD. Combining the last two equations yields (MX+MY)2=XZ2=XCβ
XD, establishing the claim.
The problems on this page are the property of the MAA's American Mathematics Competitions
