Problem:
David found four sticks of different lengths that can be used to form three noncongruent convex cyclic quadrilaterals, A,B, and C, which can each be inscribed in a circle with radius 1. Let ΟAβ denote the measure of the acute angle made by the diagonals of quadrilateral A, and define ΟBβ and ΟCβ similarly. Suppose that sinΟAβ=32β,sinΟBβ=53β, and sinΟCβ=76β. All three quadrilaterals have the same area K, which can be written in the form nmβ, where m and n are relatively prime positive integers. Find m+n.
Solution:
Let the four sticks have lengths a,b,c, and d. By renaming the sides and considering reflections, it can be assumed without loss of generality that b>c, quadrilateral A has sides a,b,c,d in that order, quadrilateral B has sides a,c, b,d in that order, and quadrilateral C has sides a,b,d,c in that order.
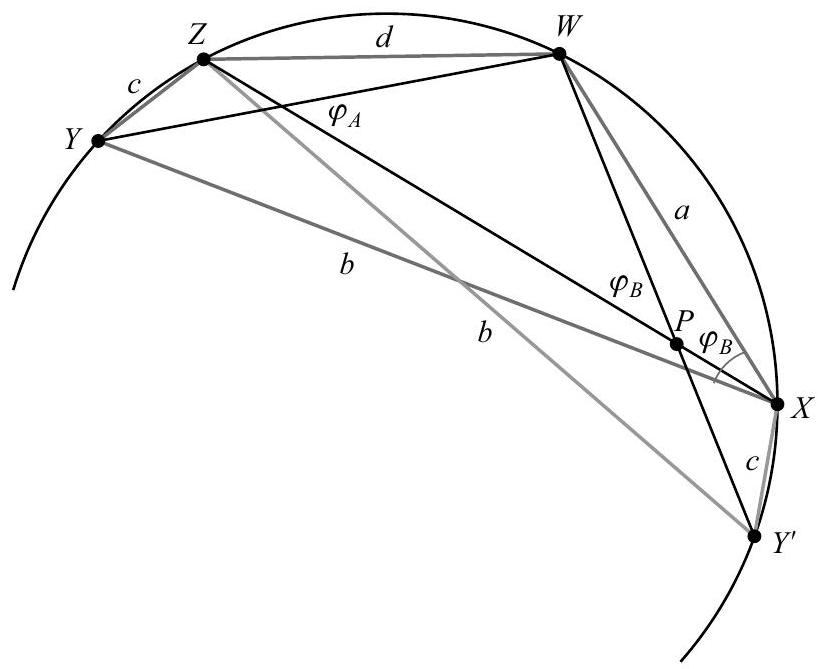
Let WXYZ denote quadrilateral A with WX=a,XY=b,YZ=c, and ZW=d, shown in the figure below. Construct point Yβ² on arcXY in the direction WβXβYβZ so that XYβ²=YZ, and let P be the intersection of XZ and WYβ². Note that WXYβ²Z has side lengths a,c,b, and d in that order, so it is congruent to quadrilateral B. Because β WPZ is half the sum of the central angles of arcsXYβ² and ZW, and β WYβ²Y is half the sum of the central angles of arcs XYβ² and ZW, it follows that β WPZ=β WYβ²Y. Because the angles ΟAβ,ΟBβ, and ΟCβ have the same sines as their supplements, it does not matter whether these angles are acute or obtuse. Hence set
ΟBβ=β WPZ=β WYβ²Y=β WXY
This means that an angle with measure ΟBβ can actually be found in an interior angle of quadrilateral A. Similarly, β ZWX=ΟCβ.
Now by the Law of Sines,
sinΟBβWYβ=sinΟCβXZβ=2
This means that
sinΟBββ sinΟCβWYβ XZβ=4
But note that the requested area is K=21βWYβ XZβ sinΟAβ. Therefore
K=2sinΟAβsinΟBβsinΟCβ=3524β
The requested sum is 24+35=59β.
Note that this result is actually a generalization of a similar result for triangles, namely that
K=2R2sinΞ±sinΞ²sinΞ³
where R is the circumradius of the triangle.
This result also follows from the fact that the area of a triangle with sides x,y, and z and circumradius R is 4Rxyzβ. The specifications in the problem are satisfied if the lengths of the sticks are approximately 0.32,0.91,1.06, and 1.82.
