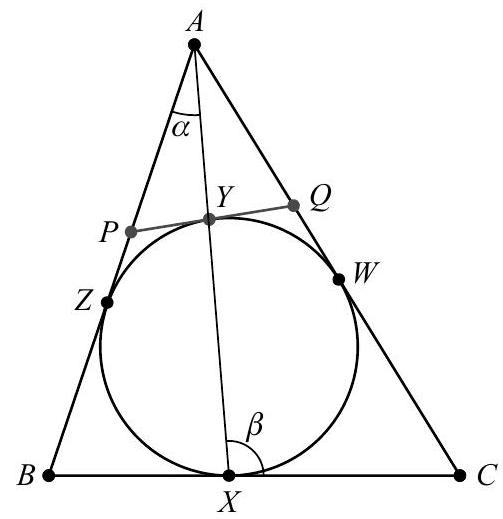
Problem:
The incircle Ο of β³ABC is tangent to BC at X. Let Yξ =X be the other intersection of AX and Ο. Points P and Q lie on AB and AC, respectively, so that PQβ is tangent to Ο at Y. Assume that AP=3,PB=4,AC=8, and AQ=nmβ, where m and n are relatively prime positive integers. Find m+n.
Solution:
Let sides AB and AC be tangent to Ο at Z and W, respectively. Let Ξ±=β BAX and Ξ²=β AXC. Because PQβ and BC are both tangent to Ο and β YXC and β QYX subtend the same arc of Ο, it follows that β AYP=β QYX= β YXC=Ξ². By equal tangents, PZ=PY. Applying the Law of Sines to β³APY yields
APAZβ=1+APZPβ=1+APPYβ=1+sinΞ²sinΞ±β
Similarly, applying the Law of Sines to β³ABX gives
ABAZβ=1βABBZβ=1βABBXβ=1βsinΞ²sinΞ±β
It follows that
2=APAZβ+ABAZβ=3AZβ+7AZβ
implying AZ=521β. Applying the same argument to β³AQY yields
2=AQAWβ+ACAWβ=AQAZβ+ACAZβ=521β(AQ1β+81β)
from which AQ=59168β. The requested sum is 168+59=227β.
The problems on this page are the property of the MAA's American Mathematics Competitions
