¶ 2018 AIME II Problem 9
Problem:
Octagon with side lengths and is formed by removing four triangles from the corners of a rectangle with side on a short side of the rectangle, as shown. Let be the midpoint of , and partition the octagon into triangles by drawing segments , and . Find the area of the convex polygon whose vertices are the centroids of these triangles.
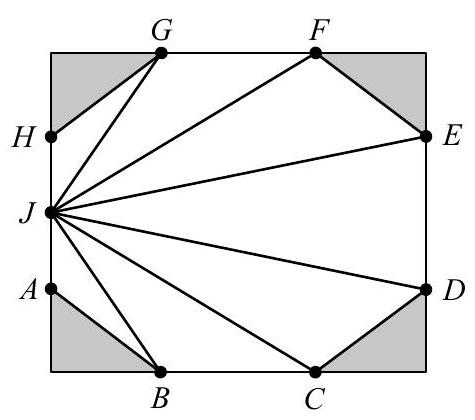
Solution:
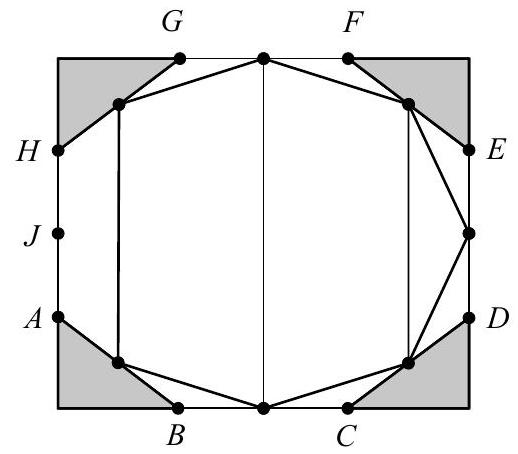
Form the convex heptagon whose vertices are the midpoints of the segments , and . The heptagon can be partitioned into two trapezoids with bases of lengths and and height , and one triangle with base length and height . Thus has area
The centroids of the triangles in the problem all lie on the line segments from the point to these midpoints, and each centroid is the distance from to its corresponding midpoint. As a result, the required heptagon whose vertices are these centroids is the image of under a dilation centered at with ratio . The requested area of is therefore .
The problems on this page are the property of the MAA's American Mathematics Competitions