Problem:
Let AB be a chord of a circle Ο, and let P be a point on the chord AB. Circle Ο1β passes through A and P and is internally tangent to Ο. Circle Ο2β passes through B and P and is internally tangent to Ο. Circles Ο1β and Ο2β intersect at points P and Q. Line PQ intersects Ο at X and Y. Assume that AP=5,PB=3,XY=11, and PQ2=nmβ, where m and n are relatively prime positive integers. Find m+n.
Solution:
Let O,O1β, and O2β denote the centers of Ο,Ο1β, and Ο2β, respectively. Points O1β and O2β lie on AO and BO, respectively, as shown in the figure below. It is clear that β³AOB,β³AO1βP, and β³BO2βP are isosceles and similar to each other, and PO2βββ₯AO and PO1βββ₯BO, and therefore PO1βOO2β is a parallelogram. In particular, O and P lie on opposite sides of line O1βO2β. Also note that P and Q lie on opposite sides of line O1βO2β.
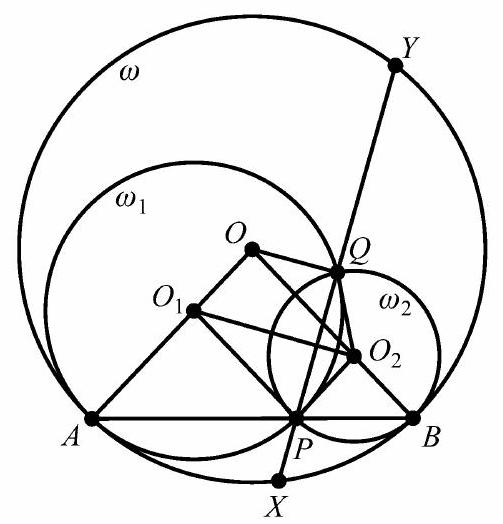
Because PO1βOO2β is a parallelogram, OO2β=O1βP=O1βQ and OO1β= O2βP=O2βQ. It follows from the last two equations that β³OO1βO2β is congruent to β³QO2βO1β by SSS. Then O1βOQO2β is a trapezoid with OQββ₯O1βO2ββ. Because PQβ is the common chord of Ο1β and Ο2β,O1βO2βββ₯PQβ. Thus OQββ₯PQβ, and therefore Q is the midpoint of XY and QX=QY=211β. By the Power of a Point Theorem,
15=APβ
PB=PXβ
PY=(QXβPQ)(PQ+QY)=4121ββPQ2
so PQ2=4121ββ15=461β. The requested sum is 61+4=65.
The problems on this page are the property of the MAA's American Mathematics Competitions