¶ 2019 AIME II Problem 1
Problem:
Points lie on the same side of line so that and are congruent with , and . The intersection of these two triangular regions has area , where and are relatively prime positive integers. Find .
Solution:
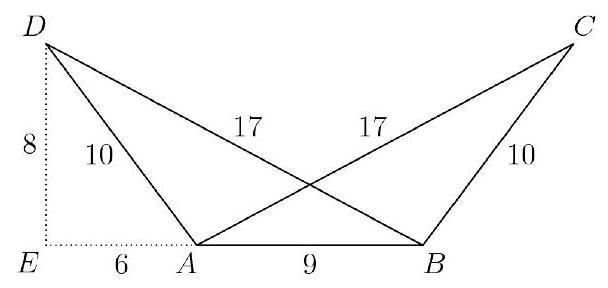
We are given that triangles and are congruent, with side lengths , , and . Since the triangles are congruent and lie on the same side of line , the figures overlap such that segment is common, and points and are located symmetrically relative to .
Consider the region of intersection between and . Since both triangles share base and are congruent, the overlapping region is a kite-shaped quadrilateral formed by connecting points and .
Construct a right triangle off each side: since is a -- triangle and is an -- triangle, the horizontal extension from point to point is , and from to is also . Since , the total base has length
Let point be the intersection of and , and let be the height from to within triangle , and be the height from to within triangle . Since triangles and are similar, their height ratio equals their base ratio:
Also, the total height is the sum of the two heights:
Substituting into this equation gives:
Now compute the area of triangle :
Hence, the desired answer is:
The problems on this page are the property of the MAA's American Mathematics Competitions