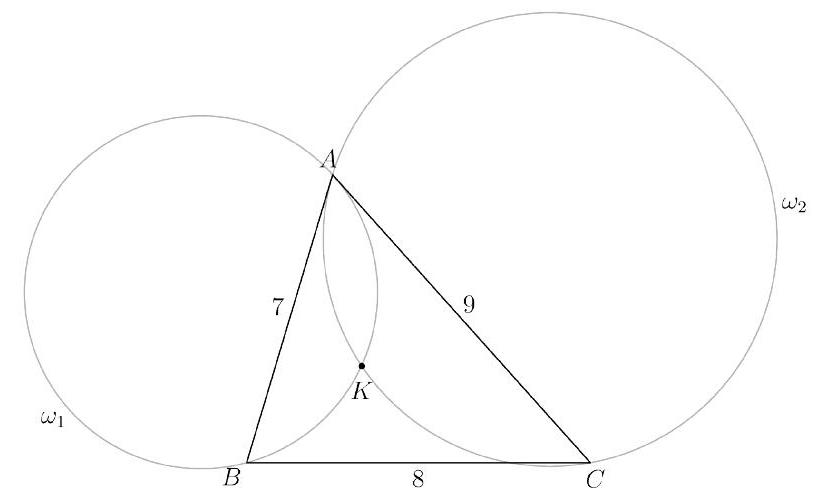
Problem:
Triangle ABC has side lengths AB=7,BC=8, and CA=9. Circle Ο1β passes through B and is tangent to line AC at A. Circle Ο2β passes through C and is tangent to line AB at A. Let K be the intersection of circles Ο1β and Ο2β not equal to A. Then AK=nmβ, where m and n are relatively prime positive integers. Find m+n.
Solution:
Notice how based off tangency that 180ββ CAB=β AKB=β AKC so we have that the angles
β AKC=β AKB.
From here, use tangency conditions again to see how
β ABK=β KAC and that similarly, β KCA=β KAB.
Thus, β³AKBβΌβ³CKA from AA similarity.
Let's create a similarity ratio.
We have that
CKAKβ=KAKBββAK2=CKβ
BK
This yields
BK=97ββ
AK,CK=98ββ
AK
Solving this we get AK=29ββ9+2=11β.
OLD SOLUTION
Notice how originally, we had that 180ββ CAB=β AKB and so we can use Law of Cosines to finish this problem off because if we find cosβ CAB, we can find cosβ AKB and use law of cosines to find AK.
Using law of cosines to find cosβ CAB, we have that
82=72+92β2β
7β
9β
cosβ CABβcosβ CAB=2111β
Now, let's finish this problem off using law of cosines
AK2+BK2β2β
AKβ
BKcosβ AKB=72
After finding that \cos \angle AKB = - \cos (180 - \angle AKB) = - \cos CAB = -\frac{11}
AK2+(97βAK)2β2β
AKβ
(97βAK)2(β2111β)=72
Note that from the tangency condition that the supplement of β CAB with respects to lines AB and AC are equal to β AKB and β AKC, respectively, so from tangent-chord,
β AKC=β AKB=180βββ BAC
Also note that β ABK=β KAC(β), so β³AKBβΌβ³CKA. Using similarity ratios, we can easily find
AK2=BKβKC
However, since AB=7 and CA=9, we can use similarity ratios to get
BK=97βAK,CK=79βAK
Now we use Law of Cosines on β³AKB : From reverse Law of Cosines, cosβ BAC=2111ββΉcos(180βββ BAC)= β AKB=β2111β Giving us
AK2+8149βAK2+2722βAK2=49βΉ81196βAK2=49AK=29ββ
so our answer is 9+2=11β.
(β) Let O be the center of Ο1β. Then β KAC=90ββ OAK=90β21β(180ββ AOK)=2β AOKβ=β ABK. Thus, β ABK=β KAC.
The problems on this page are the property of the MAA's American Mathematics Competitions
