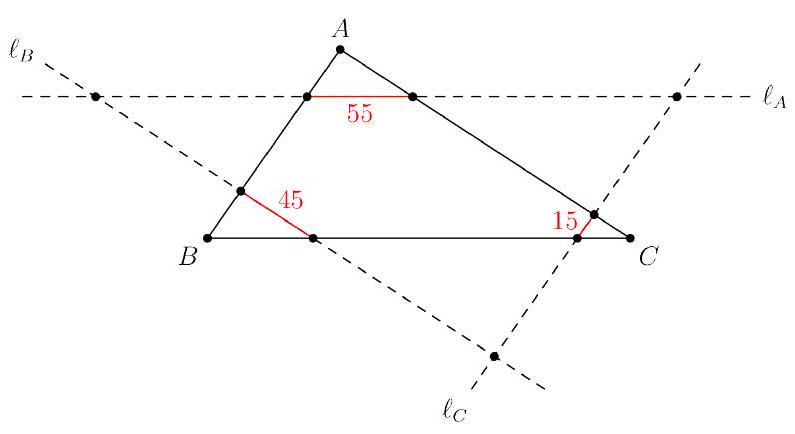
Problem:
Triangle ABC has side lengths AB=120,BC=220, and AC=180. Lines ℓA,ℓB, and ℓC are drawn parallel to BC,AC, and AB, respectively, such that the intersection of ℓA,ℓB, and ℓC with the interior of △ABC are segments of length 55,45 , and 15 , respectively. Find the perimeter of the triangle whose sides lie on ℓA,ℓB, and ℓC.
Solution:
Let the lines ℓA,ℓB,ℓC intersect triangle ABC as follows: let D be the intersection of ℓC with side AB, E the intersection of ℓC with side BC, F the intersection of ℓB with side BC, G the intersection of ℓB with side AC, H the intersection of ℓA with side AC, and I the intersection of ℓA with side AB. Let the triangle formed by the intersections of these cevians be △XYZ, where X lies closest to side BC, Y closest to AC, and Z closest to AB.
We wish to compute the perimeter DX+XE+FY+YG+HZ+ZI+115, where the lengths EF=15, GH=55, and ID=45 contribute 15+55+45=115 units already.
From triangle similarity, we are given that △AHG∼△BID with scale factor 2, so HA=BI=30 and BD=HG=55. Since △EFC∼△ABC, we also find FC=245 and EC=255.
Now consider the similar triangles involved in computing the remaining segments. In △EFC∼△YFG, the ratio of similarity gives:
FY+YG=FCGF⋅(EF+EC)=45225⋅(15+255)=5⋅285=2425
Likewise, in △EFC∼△EXD, we compute:
DX+XE=ECDE⋅(EF+FC)=55275⋅(15+245)=5⋅275=2375
Finally, in △BID∼△HIZ, the similarity gives:
HZ+ZI=BIIH⋅(ID+BD)=2⋅(45+55)=200
Adding all parts of the perimeter:
DX+XE+FY+YG+HZ+ZI+115=(2375+2425+200)+115=600+115=715
The problems on this page are the property of the MAA's American Mathematics Competitions