¶ 2020 AIME I Problem 6
Problem:
A flat board has a circular hole with radius and a circular hole with radius such that the distance between the centers of the two holes is . Two spheres with equal radii sit in the two holes such that the spheres are tangent to each other. The square of the radius of the spheres is , where and are relatively prime positive integers. Find .
Solution:
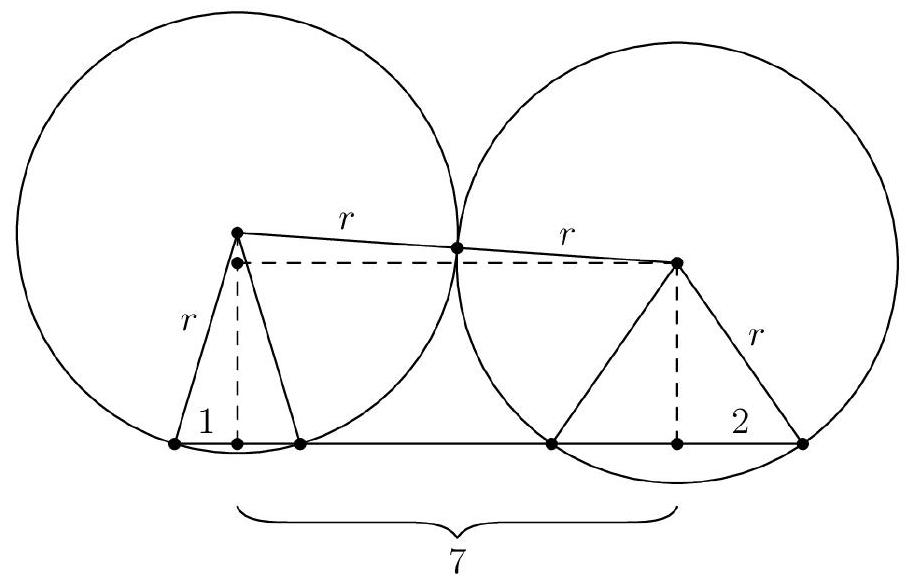
Let the common radius be . Consider a cross section of the sphere resting in a circular hole of radius . In this cross section, we have a circle (representing the sphere) with a chord of length corresponding to the diameter of the hole. Draw the perpendicular bisector of the chord, which passes through the center of the circle. Connecting the center of the circle to the endpoint of the chord forms a right triangle with hypotenuse and one leg of length . By the Pythagorean theorem, the vertical distance from the center to the chord — that is, the portion of the sphere above the hole — is .
The second sphere follows similarly, with the portion extending above the hole having height , since the radius of its hole is . Now, consider a cross section of the entire setup, reducing the problem to two dimensions. Connect the centers of the two spheres; this segment forms the hypotenuse of a right triangle whose horizontal leg is the distance between the holes, which is (as given). The vertical leg of the triangle is the difference between the heights of the parts of the two spheres that lie above their respective holes, which is .
Now we can set up an equation in terms of with the Pythagorean theorem:
Simplifying,
Therefore, our answer is .
The problems on this page are the property of the MAA's American Mathematics Competitions