Problem:
Convex pentagon ABCDE has side lengths AB=5,BC=CD=DE=6, and EA=7. Moreover, the pentagon has an inscribed circle (a circle tangent to each side of the pentagon). Find the area of ABCDE.
Solution:
Let Ο be the inscribed circle, I be its center, and r be its radius. The area of ABCDE is equal to its semiperimeter, 15, times r, so the problem is reduced to finding r. Let a be the length of the tangent segment from A to Ο, and analogously define b,c,d, and e. Then a+b=5,b+c=c+d=d+e=6, and e+a=7, with a total of a+b+c+d+e=15. Hence a=3,b=d=2, and c=e=4. It follows that β B=β D and β C=β E. Let Q be the point where Ο is tangent to CD. Then β IAE=β IAB=21ββ A. The sum of the internal angles in polygons ABCQI and AIQDE are equal, so β IAE+β AIQ+β IQD+β D+β E=β IAB+β B+β C+β CQI+β QIA, which implies that β AIQ must be 180β. Therefore points A,I, and Q are collinear.
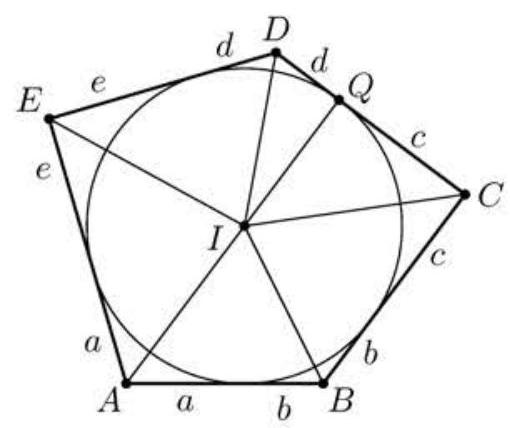
Because AQββ₯CD, it follows that
AC2βAD2=CQ2βDQ2=c2βd2=12.
Another expression for AC2βAD2 can be found as follows. Note that tan(2β Bβ)=2rβ and tan(2β Eβ)=4rβ, so
cos(β B)=1+tan2(2β Bβ)1βtan2(2β Bβ)β=4+r24βr2β
and
cos(β E)=1+tan2(2β Eβ)1βtan2(2β Eβ)β=16+r216βr2β
Applying the Law of Cosines to β³ABC and β³AED gives
AC2=AB2+BC2β2β
ABβ
BCβ
cos(β B)=52+62β2β
5β
6β
4+r24βr2β
and
AD2=AE2+DE2β2β
AEβ
DEβ
cos(β E)=72+62β2β
7β
6β
16+r216βr2β
Hence
12=AC2βAD2=52β2β
5β
6β
4+r24βr2ββ72+2β
7β
6β
16+r216βr2β,
yielding
2β
7β
6β
16+r216βr2ββ2β
5β
6β
4+r24βr2β=36
equivalently
7(16βr2)(4+r2)β5(4βr2)(16+r2)=3(16+r2)(4+r2)
Substituting x=r2 gives the quadratic equation 5x2β84x+64=0, with solutions 542β38β=54β and 542+38β=16. The solution r2=54β corresponds to a five-pointed star, which is not convex. Indeed, if r<3, then tan(2β Aβ),tan(2β Cβ), and tan(2β Eβ) are less than 1, implying that β A,β C, and β E are acute, which cannot happen in a convex pentagon. Thus r2=16 and r=4. The requested area is 15β
4=60β.
OR
Define a,b,c,d,e, and r as in the first solution. Then, as above, a=3,b=d=2,c=e=4, β B=β D, and β C=β E. Let Ξ±=2β Aβ,Ξ²=2β Bβ, and Ξ³=2β Cβ. It follows that 540β=2Ξ±+4Ξ²+4Ξ³, so 270β=Ξ±+2Ξ²+2Ξ³. Thus
tan(2Ξ²+2Ξ³)=tanΞ±1β
tan(Ξ²)=2rβ,tan(Ξ³)=4rβ, and tan(Ξ±)=3rβ. By the Tangent Addition Formula,
tan(Ξ²+Ξ³)=8βr26rβ
and
tan(2Ξ²+2Ξ³)=1β(8βr2)236r2β8βr212rββ=(8βr2)2β36r212r(8βr2)β
Therefore
(8βr2)2β36r212r(8βr2)β=r3β
which simplifies to 5r4β84r2+64=0. Then the solution proceeds as in the first solution.
OR
Define a,b,c,d,e, and r as in the first solution. Note that
arctan(raβ)+arctan(rbβ)+arctan(rcβ)+arctan(rdβ)+arctan(reβ)=180β.
Hence
Arg(r+3i)+2β
Arg(r+2i)+2β
Arg(r+4i)=180β.
Therefore
Im((r+3i)(r+2i)2(r+4i)2)=0.
Simplifying this equation gives the same quadratic equation in r2 as above.
The problems on this page are the property of the MAA's American Mathematics Competitions