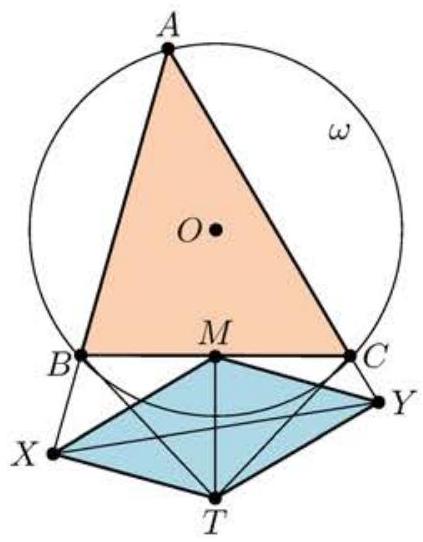
Problem:
Let β³ABC be an acute scalene triangle with circumcircle Ο. The tangents to Ο at B and C intersect at T. Let X and Y be the projections of T onto lines AB and AC, respectively. Suppose BT=CT=16, BC=22, and TX2+TY2+XY2=1143. Find XY2.
Solution:
Let M denote the midpoint of BC. The critical claim is that M is the orthocenter of β³AXY, which has the circle with diameter AT as its circumcircle. To see this, note that because β BXT=β BMT=90β, the quadrilateral MBXT is cyclic. Thus
β MXA=β MXB=β MTB=90βββ TBM=90βββ A,
implying that MXβ₯AC. Similarly, MYβ₯AB. In particular, MXTY is a parallelogram.
Hence, by the Parallelogram Law,
TM2+XY2=2(TX2+TY2)=2(1143βXY2)
But TM2=TB2βBM2=162β112=135. Therefore
XY2=31β(2β
1143β135)=717β
The problems on this page are the property of the MAA's American Mathematics Competitions
