¶ 2020 AIME II Problem 2
Problem:
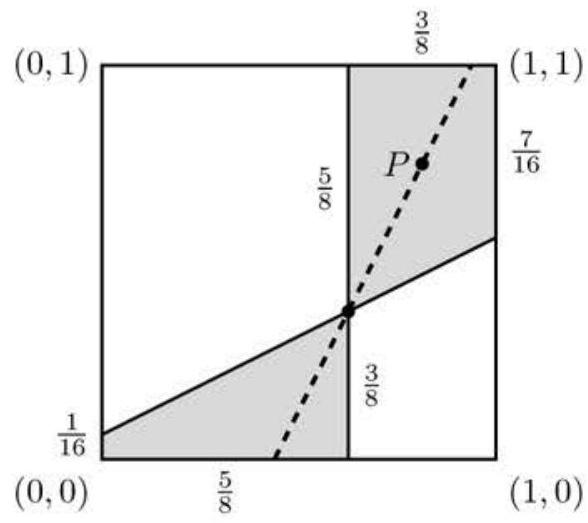
Let be a point chosen uniformly at random in the interior of the unit square with vertices at , and . The probability that the slope of the line determined by and the point is greater than can be written as , where and are relatively prime positive integers. Find .
Solution:
Let us find the equation of the line through the fixed point with slope . Using point-slope form, we get the equation . The slope of the line joining a random point in the unit square to this fixed point is greater than precisely when lies above this line for or below the line for .
These two regions form two trapezoids within the unit square. We compute the total area of these trapezoids to find the desired probability.
For from to , the -values on the line go from to . The area of the first trapezoid is .
For from to , the -values on the line go from to . The area of the second trapezoid is .
Adding these areas gives the total probability:
The answer is .
The problems on this page are the property of the MAA's American Mathematics Competitions