¶ 2020 AIME II Problem 7
Problem:
Two congruent right circular cones each with base radius and height have axes of symmetry that intersect at right angles at a point in the interior of the cones a distance from the base of each cone. A sphere with radius lies inside both cones. The maximum possible value for is , where and are relatively prime positive integers. Find .
Solution:
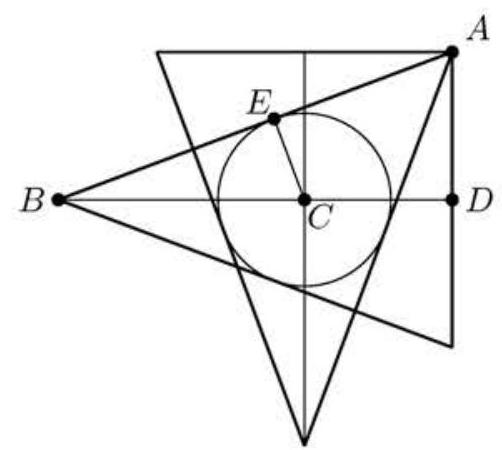
Consider a cross-sectional view of the configuration through a plane containing both axes of symmetry of the cones. The largest possible inscribed sphere will be tangent to the lateral sides of both cones. Consequently, its center must lie at the intersection of their axes of symmetry.
Let point denote the meeting point of the two cone bases, and let be the center of the sphere. Denote as the vertex of one cone and as the center of its base, so that is the axis of symmetry. Let the sphere be tangent to at point .
Observe that and are similar right triangles because both share corresponding angles formed by the tangency and cone axes. This yields the proportional relationship:
Note that , so we substitute to get:
We are given , , and . Therefore:
The final answer is the sum of the numerator and denominator: .
The problems on this page are the property of the MAA's American Mathematics Competitions