¶ 2022 AIME I Problem 10
Problem:
Three spheres with radii and are mutually externally tangent. A plane intersects the spheres in three congruent circles centered at , and , respectively, and the centers of the spheres all lie on the same side of this plane. Suppose that . Find .

Solution:
Let be the plane determined by the centers of the spheres. Denote and as the centers of the spheres with radii and , respectively. We consider a cross-section of the configuration that includes both points and , and thus contains the spheres centered at and , but excludes the third sphere. This setup is illustrated below:
.jpg)
Since the cross-section intersects the two spheres in congruent circles, their radii must be equal. From the given information, the distance between points and is . The quadrilateral forms a trapezoid. We drop a perpendicular from to the line segment , meeting it at point , which creates a right triangle. Let the length of this perpendicular be , and let the distance from to be . Then by the Pythagorean Theorem, we have:
Since and are opposite sides of a rectangle, they are equal in length. This gives the equation .
Squaring both sides:
121 - r^2 = 169 - r^2 + 16 - 8\sqrt
Subtracting from both sides and simplifying:
So:
This also tells us that implies . Since , we conclude that .
Taking a cross-section that contains and , which contains these two spheres but not the third, we obtain the following diagram:
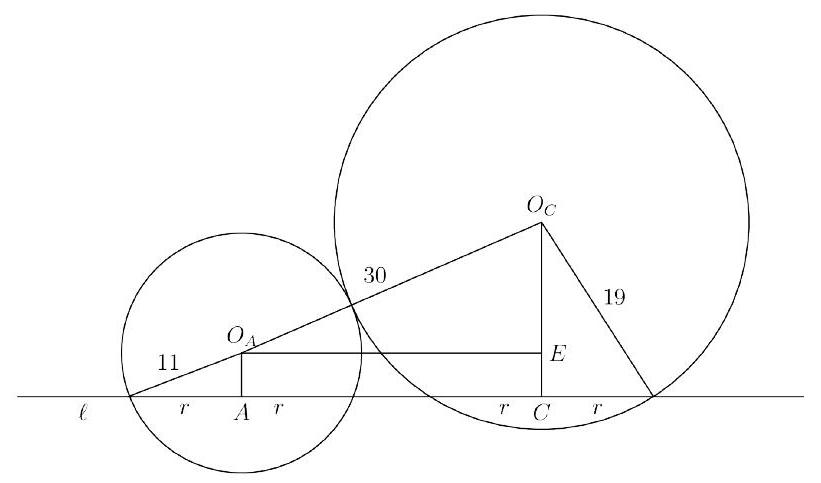
The distance from point to the center is given by . Since we previously found , the vertical distance from to is .
Now applying the Pythagorean Theorem to triangle , we find:
O_AE = \sqrt{30^2 - 12^2} = \sqrt{900 - 144} = \sqrt
Thus, the square of the length between and , which is also equal to , is .
The problems on this page are the property of the MAA's American Mathematics Competitions