¶ 2022 AIME I Problem 11
Problem:
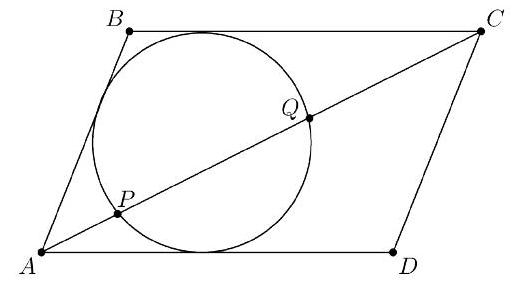
Let be a parallelogram with . A circle tangent to sides , and intersects diagonal at points and with , as shown. Suppose that , and . Then the area of can be expressed in the form , where and are positive integers, and is not divisible by the square of any prime. Find .
Solution:
Suppose the points of tangency from the circle to AD and BC are and respectively.
Then by Power of a Point, we have that
Similarly, we have that
We can then find the length of using pythagorean theorem.
In particular, Let's draw the foot of the altitude from C to AD.
Let that point be W.
Then we have that
Notice that
And so we have that
Then, we have that
Thus, we've found the height, and notice that if we find the length of the base we are done.
Let
Notice how then that would make DW , and that using the properties of tangents,
Using pythagorean theorem on triangle , we have that
This yields x = \frac{9}
The area would then be
The problems on this page are the property of the MAA's American Mathematics Competitions