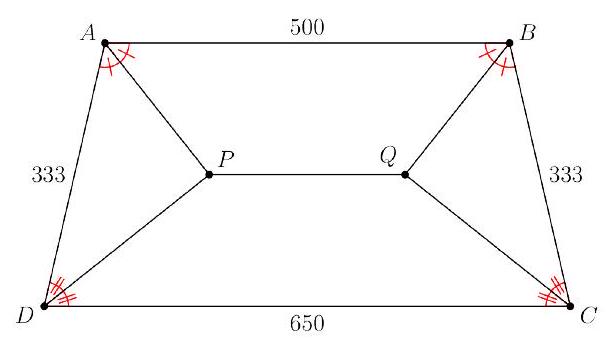
Problem:
In isosceles trapezoid ABCD, parallel bases AB and CD have lengths 500 and 650 , respectively, and AD= BC=333. The angle bisectors of ∠A and ∠D meet at P, and the angle bisectors of ∠B and ∠C meet at Q. Find PQ.
Solution:
Extend PQ in both directions. Call the intersection of PQ and AD as E, and the intersection of PQ and BC as F. As trapezoid ABCD is isosceles, PQ∥AB∥CD. By interior angles, ∠PAB=∠APE and since PA is the angle bisector of ∠DAB, ∠PAB=∠PAD. This proves △EPA and △EPD are isosceles. As this happens on both sides of the trapezoid, EF is the midline of the trapezoid.
Now, EA=ED=EP=2AD, and as AD=333, EP=333/2. By symmetry, FQ=333/2 as well. As EF is the midline, EF=2AB+CD. We write EF=EP+PQ+QF, and we know EP+QF=333. Using the given values for AB and CD, we can calculate PQ=242.
The problems on this page are the property of the MAA's American Mathematics Competitions
