¶ 2022 AIME I Problem 5
Problem:
A straight river that is meters wide flows from west to east at a rate of meters per minute. Melanie and Sherry sit on the south bank of the river with Melanie a distance of meters downstream from Sherry. Relative to the water, Melanie swims at meters per minute, and Sherry swims at meters per minute. At the same time, Melanie and Sherry begin swimming in straight lines to a point on the north bank of the river that is equidistant from their starting positions. The two women arrive at this point simultaneously. Find .
Solution:
Let denote the number of minutes each swimmer is in the water before they meet. Let the meeting point be , and define to be the point both swimmers aim for to account for the river’s current.
Since Melanie swims against a current for minutes, she will be pushed meters downstream during that time. To land at , she must aim meters upstream of it—so she targets point , which lies meters upstream from . Similarly, Sherry is carried meters downstream over minutes, so she must also aim at point to arrive at .
Now consider a modified version of the scenario where the river has no current. In this case, both swimmers would swim directly to point in minutes. Melanie swims in that time, and Sherry swims . Let represent the distance between the swimmers’ starting points. The triangle formed by Melanie’s path, Sherry’s path, and the base models this setup.
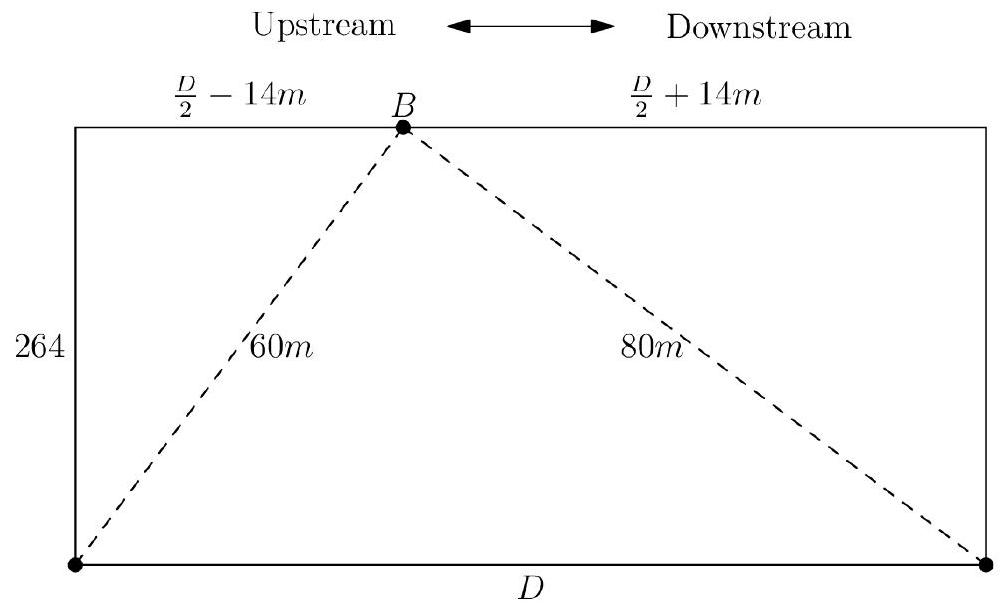
Assuming symmetry, the horizontal component of Melanie’s path is , and that of Sherry’s is . Applying the Pythagorean Theorem to both triangles gives:
Subtracting the first from the second:
Using the difference of squares:
Substitute back into the first equation:
Finally, the distance between starting points is:
.
The problems on this page are the property of the MAA's American Mathematics Competitions