¶ 2022 AIME I Problem 8
Problem:
Equilateral triangle is inscribed in circle with radius . Circle is tangent to sides and and is internally tangent to . Circles and are defined analogously. Circles , and meet in six points-two points for each pair of circles. The three intersection points closest to the vertices of are the vertices of a large equilateral triangle in the interior of , and the other three intersection points are the vertices of a smaller equilateral triangle in the interior of . The side length of the smaller equilateral triangle can be written as , where and are positive integers. Find .
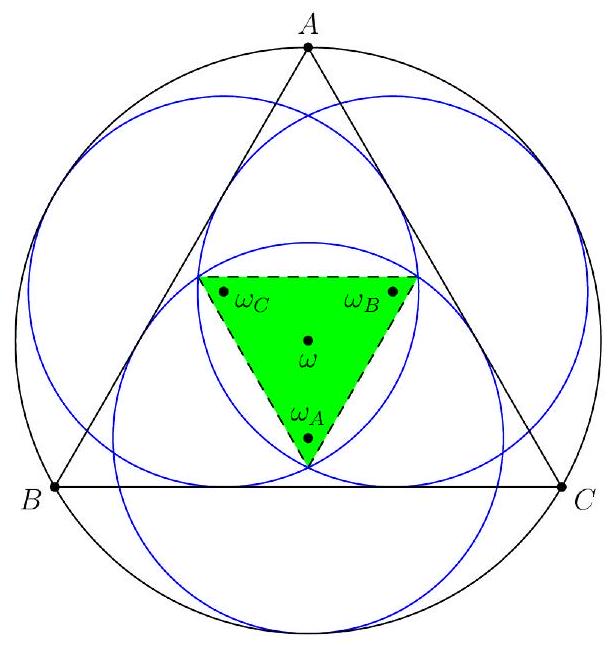
Solution:
We extend sides and beyond point to points and respectively, in such a way that the circle becomes the incircle of triangle .
.jpg)
Since the diameter of the circle equals the height of the triangle, the height is . In an equilateral triangle, the incenter coincides with the centroid, which lies one-third of the way from each vertex to the base. Thus, the inradius is one-third the height, or . It follows that the radius of each of the smaller circles is .
Let be the center of the large circle , and place it at the origin of the coordinate plane. The center of circle lies directly below at a distance of , so its coordinates are .
Rotating this point counterclockwise about the origin gives the center of . Since the distance from the origin is preserved, the center of lies units from at an angle of above the horizontal. This gives its coordinates as . By symmetry, the center of is located at .
The upper left and right circles intersect at two points, the lower of which is . The equations of these two circles are:
Subtract the two equations to get . Plugging back in to the first equation, we have . We take the lower solution to get .
Notice that it is easy to find as they lie on the same vertical, is degrees so we can make use of triangles, and because is the center of triangle . We can draw the diagram as such:
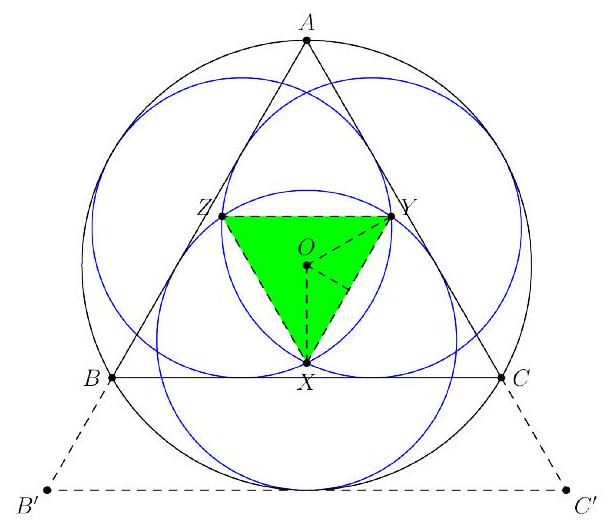
Note that . It follows that
Finally, the answer is .
The problems on this page are the property of the MAA's American Mathematics Competitions