¶ 2023 AIME I Problem 13
Problem:
Each face of two noncongruent parallelepipeds is a rhombus whose diagonals have lengths and . The ratio of the volume of the larger of the two polyhedra to the volume of the smaller is , where and are relatively prime positive integers. Find . A parallelepiped is a solid with six parallelogram faces such as the one shown below.
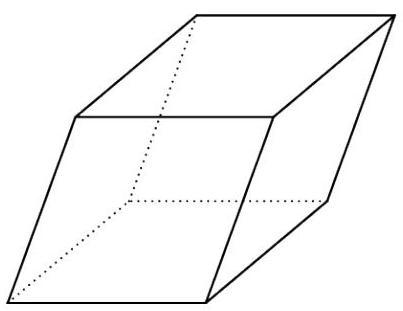
Solution:
Suppose is the smaller angle of each rhombus, placing them "flat" like in the image.
Let's denote X be the point on the plane that has angles of degrees. In the diagram above, let's set X as the bottom left point of the plane, and set Y as the point on the upper part of the rhombus next to X.
Let the foot of the altitude of X to the bottom plane as P. Suppose the foot of P to one of X's sides be W.
Notice that XP bisects angle , and we write
By Pythagorean theorem, notice that we have
Let's create variables for lengths and then simplify.
if , then the rhombus has side lengths x and we'd have that and
Then, expanding using pythagorean theorem, we'd have that
Simplifying this and using the identities , we can rewrite this as
Drawing out the diagonals and creating right triangles gives us the following
Using double/half angle identity formulas yield and simplifying this expression off fully yields , and the ratio of the larger to the smaller would simply be the reciprocal to make the answer greater than 1 or
The problems on this page are the property of the MAA's American Mathematics Competitions