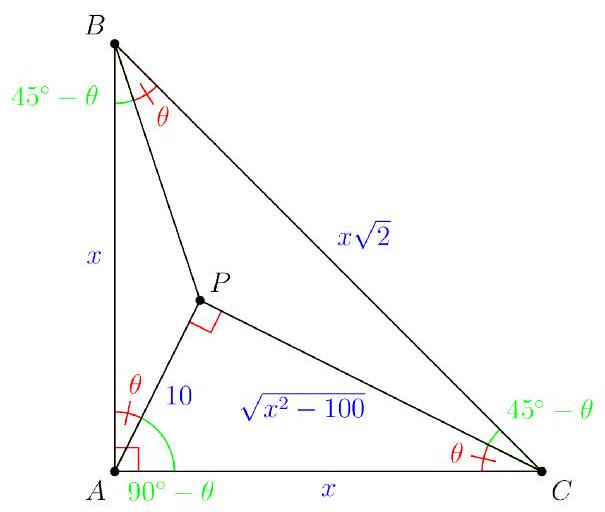
Problem:
Let β³ABC be an isosceles triangle with β A=90β. There exists a point P inside β³ABC such that β PAB=β PBC=β PCA and AP=10. Find the area of β³ABC.
Solution:
Let AB=AC=x and β PAB=β PBC=β PCA=ΞΈ, from which BC=x2β,β PAC=90ββΞΈ, and β APC=90β. By the Pythagorean Theorem on right β³APC, we have PC=x2β100β.
Moreover, we have β PBA=β PCB=45ββΞΈ, as shown below:
Note that β³PABβΌβ³PBC by the AA Similarity. The ratio of similitude is PBPAβ=PCPBβ=BCABβ, or
PB10β=x2β100βPBβ=x2βxβ=2β1β
From PB10β=2β1β, we get PB=102β. It follows that from PB10β=x2β100βPBβ, we get x2=500.
.jpg)
