¶ 2023 AIME II Problem 6
Problem:
Consider the L-shaped region formed by three unit squares joined at their sides, as shown below. Two points and are chosen independently and uniformly at random from inside the region. The probability that the midpoint of also lies inside this L-shaped region can be expressed as , where and are relatively prime positive integers. Find .
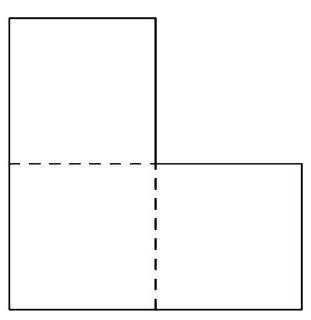
Solution:
We approach this by computing the complement. The only configuration that places the midpoint of two randomly chosen points outside the L-shaped region is when one point lies in the top square and the other lies in the right square. This occurs with a probability of .
Let the point in the top square be at coordinates , and the point in the right square be at , where . Then the midpoint of these two points is
For the midpoint to lie outside the L-shape, both coordinates of the midpoint must be greater than , so:
Each of these inequalities occurs with probability by symmetry over . Hence, the probability that both conditions are satisfied simultaneously is .
Therefore, the probability that the midpoint lies inside the L-shape is .
The final answer is:
The problems on this page are the property of the MAA's American Mathematics Competitions